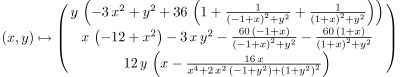Snow Sculpting with Mathematica
Day Zero Day Zero
Day One
Day Two
Day Three
Day Four
Day Five
Background
How does one find a minimal surface approximating a given shape? One way would be to take the boundary contour, in this case three interlinked circles, and solve the Plateau problem. In reality, this can be achieved by putting a wireframe model of the boundary contour into soap and pulling it out. The soapfilm spanned by the wireframe will be a minimal surface. To find equations for the surface is much harder. A few things usually help here quite a bit: First, symmetries are very important. It looked as if the Longhurst sculpture had two lines of symmetry, namely the horizontal and vertical axes. Rotating the surface about these lines would carry it into itself.
Also, mathemematicians like it when their objects are complete. The Longhurst sculpture has a boundary, but is was conceivable that it was part of much larger surface without boundary, just as a disk is a part of the more complete plane in which it resides. Such complete minimal surfaces are much better understood than the general minimal surface.
So we made the assumptions that the surface we were looking for actually had these symmetries and was part of a complete surface.
Using this, we could prove that there is essentially only one complete surface satisfying all geometric properties which were visible in the Longhurst sculpture. However, there was no reason to believe that this abstract mathematical minimal surface should look similar to Longhurst's original sculpture.
It was a big surprise that there is a good amount of similarity. Below is a front view of the surface with the straight symmetry lines on it.
Mathematica image of Longhurst scuplture
For the curious, below is the formula used to create the above pictures:
  Formula