Solution
The key is using the ideas of Benford's Law, which does apply to powers of 2 — but not as simply as I thought. Here, log means base-10 logarithm.
Benford's Law states that the probability of the leading digit (no rounding) being d is log[(d + 1)/d]. For more digits, one uses the "strong form" of the law, which states that, for a data set X, the set fractionalpart(log X) is uniformly distributed in [0, 1).
So the probability of a number (ignoring powers of 10) lying between, say, 4.5 and 5.5 is log[11/2] − log[9/2] or log[(11/2)/(9/2)], or log(11/9). This gives the probability that the rounded number begins with a 5. This formula, log[(2d + 1)/(2d − 1)], applies to all digits d = 2, 3, 4, 5, 6, 7, 8, 9.
But d = 1 is different, because of the wraparound issue: 283 = 9671406556917033397649408, which rounds to 10000000000000000000000000. The probability of leading with a 1 is therefore [log(10) − log(19/2)] + [log(3/2) − log(1)] = log[(10/(19/2))*(3/2)] = log(30/19). Of course, this last could also be obtained by subtracting the probabilities for all the other digits from 1.
So the probability of a 2 is about 0.2218, and a 1 is 0.1984, which makes 2 the most likely digit.
All these ideas work just as well in base b. Here is a table of digit probabilities in several bases:
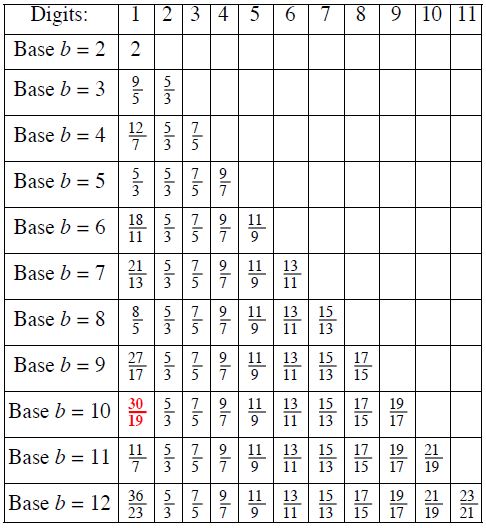
David Broadhurst (Open University, UK) made the surprising discovery that, in base 5, the probability of a 1 EXACTLY equals the probability of a 2; both equal 1 − log5(3). Also, for bases less than 5, the most likely digit is 1; for bases greater than 5, the most likely digit is 2. Of course, all this applies to any data set that follows the strong Benford Law (in the appropriate base).
Now, to the delicate point of why the powers of 2 satisfy the strong Benford Law. It is not too hard to prove that the fractional parts of {n*log(2)} are dense in the unit interval: one can prove it using the pigeonhole principle, as in the StackExchange thread "Multiples of an irrational number forming a dense subset".
But uniformity is a stronger result, and no simple proof is known. A complete proof is Corollary 1.5 (page 13) from Steuding's Ergodic Number Theory.
A proof can also be found in Theorem of 1 of Ken Ross's nice paper, "Benford's Law, a growth industry", American Mathematical Monthly 118 (2011) 571-583.
But this is really inadequate for this problem's solution, so my apologies that this is not really a problem that can be done completely by the intended audience. Still, many solvers (Broadhurst, John Sullivan, Abraham Kunin, John Snyder, Stephen Morris, and Joseph DeVincentis) did as I did and just assumed that the strong Benford's Law is valid for the powers of 2. This problem was inspired by two recent books about Benford's Law, a subject that has fascinated me for some time. The books are:
-
Benford's Law, Theory & Applications, edited by Steven J. Miller, Princeton Univ. Press
-
An Introduction to Benford's Law, by Arno Berger and Theodore Hill, Princeton Univ. Press
The collection of applications discussed in Miller's work is quite extensive and interesting; here is a sample chapter.
Dan Velleman has just worked out an elementary proof of the Uniform Distribution Theorem. It seems to be unpublished, though David Speyer of the University of Michigan had worked out the same proof some years ago. While the advanced proofs give more info and are more general, there is virtue in a completely elementary proof such as Dan's, now available as a PDF.
I have not yet seen it, but Alberto Zorzi recently published this online (not yet in print): "An Elementary Proof for the Equidistribution Theorem."
[Back to Problem 1211]
© Copyright 2015 Stan Wagon. Reproduced with permission.