Problem of the Week 1206
Cubic Snake
Solution Notes
I know of no prior literature on this version, but as Danny Lichtblau pointed out, this problem does bear resemblance to the Snake-in-a-Box problem.
The problem, which was first raised in a puzzle column by Terry
Stickels, was posed for 3 × 3 × 3. Joseph DeVincentis, Larry Carter,
Stephen Meskin, and John Snyder found solutions. The longest possible
snake has length 25, the path of which appears here:
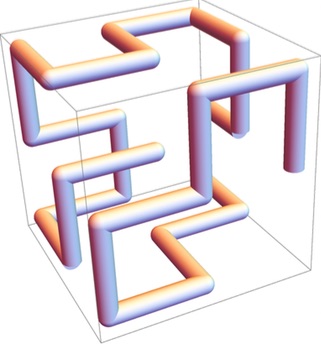
Using base-3 notation, a length-5 snake can be given as
|
14,
|
11,
|
10,
|
1,
|
4,
|
|
5,
|
2,
|
3,
|
12,
|
15,
|
|
6,
|
9,
|
18,
|
17,
|
8,
|
|
7,
|
16,
|
13,
|
22,
|
19,
|
|
20,
|
23,
|
24,
|
27,
|
26
|
In coordinates:
{1, 1, 2}, {1, 0, 2}, {1, 0, 1}, {0, 0, 1}, {0, 1, 1},
{0, 1, 2}, {0, 0, 2}, {0, 1, 0}, {1, 1, 0}, {1, 2, 0},
{0, 2, 0}, {1, 0, 0}, {2, 0, 0}, {1, 2, 2}, {0, 2, 2},
{0, 2, 1}, {1, 2, 1}, {1, 1, 1}, {2, 1, 1}, {2, 0, 1},
{2, 0, 2}, {2, 1, 2}, {2, 2, 0}, {0, 0, 0}, {2, 2, 2}
DeVincentis, Meskin, and Carter all proved that 25 is the maximum. DeVincentis also found, by hand, a path of length 81 in the 3 × 3 × 3 × 3 cube. And Carter found a full path in the 4 × 4 × 4:
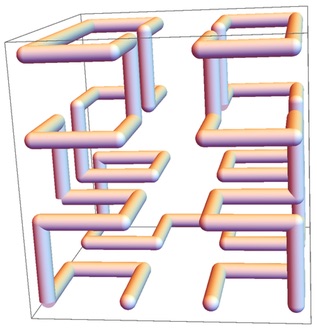
Carter's method extends to n × n × n in the case of even n. So 5 × 5 × 5 remained unresolved.
Here is Carter's proof that 25 is maximum for 3 × 3 × 3.
First, alternately color the cubies black and white, with the corners black. There are 14 black cubies and 13 white. Of the 14 blacks, 8 are corner pieces and 6 are centers of exterior faces. I'll call these corner and face cubie, respectively. The remaining (white) cubies are the 12 "edge" and one "center" cubie.
Whenever you are at a corner, because you need to change directions every turn, the next black cubie you hit will be a face cubie. There are only 6 face cubies, so a path can hit at most 7 of the 8 corners. Thus it will hit at most 13 of the 14 black cubies.
Now, if a path goes through the center, then it must both enter and leave the center through a face cubie. Thus, either:
-
the path avoids the (white) center, so it hits at most 12 of the 13 whites and, from above, 13 of the 14 blacks, and so at most 25.
-
it goes through the center, but does not start or end at the center, in which case the sequence of black cubies cannot alternate corner and face pieces: there would be two consecutive face pieces before and after the center. But alternating corners and faces was the only way to get 13 black cubies on the path. So it has at most 12 black cubies and 13 white, for a max of 25.
-
it starts at the center (or ends, by symmetry). Then the only way to get 26 is WBWB....WB. But the 13 blacks here would have to be face, corner,..., face, for a total of seven face cubies — and there are only 6.
QED.
For 4 × 4 × 4 and higher evens, Carter's idea is to go up a 2 × 2 column, then down in a neighboring column, then up the next one, and so on, until all is covered. This is not very precise — one has choices and must be clear about what to do at each choice — but it seems believable. The odd case beyond 3 was a bit of a mystery.
I saw that this could be set up as an ILP (integer-linear programming) problem, where one adds constraints to enforce the no-three-in-a-line rule. The problem is that asking that every point have degree 2 (except the ends) can lead to disjoint cycles. But a standard technique is cycle-killing. One cannot add constraints in advance to kill all possible cycles (there are too many: 260), but one can kill them as they arise. This found a path of length 124 that I thought might be optimal.
But then I carried on, using a trick suggested by Rob Pratt to avoid the problem of having to guess the start/finish points. The idea is to add a new dummy vertex and connect it to all 125 vertices, but letting each new edge have 0 cost. Now we ask that every vertex have degree 2. So then the cycle-killing iterations led to a cycle-free solution of length 125 in just six iterations.
If you did not follow this or have no idea how ILP might work, have a look at this long snake:
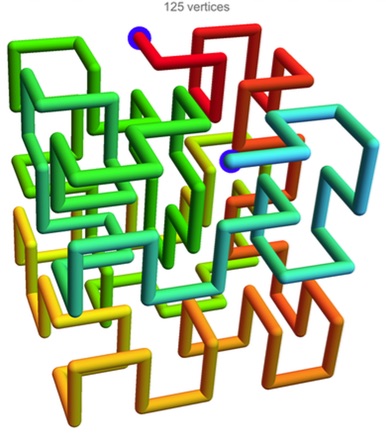
This is such a pretty little object that I might get a 3D-printed model.
So perhaps, for every n, the n × n × n grid has a full wiggling path (length n³), with the sole exception of n = 3. If 5 × 5 × 5 has enough wiggle room to do it, it would seem that the same would be true of 7 × 7 × 7, and larger. And note that the 2 × 2 × 2 case works, too.
If you want to draw or make your own, the coordinates are:
{2, 0, 0}, {2, 1, 0}, {3, 1, 0}, {3, 1, 1}, {3, 0, 1},
{3, 0, 0}, {4, 0, 0}, {4, 0, 1}, {4, 1, 1}, {4, 1, 0},
{4, 2, 0}, {3, 2, 0}, {3, 2, 1}, {4, 2, 1}, {4, 2, 2},
{3, 2, 2}, {3, 2, 3}, {4, 2, 3}, {4, 2, 4}, {4, 3, 4},
{4, 3, 3}, {4, 4, 3}, {4, 4, 4}, {3, 4, 4}, {3, 4, 3},
{3, 3, 3}, {3, 3, 4}, {2, 3, 4}, {2, 3, 3}, {2, 4, 3},
{2, 4, 4}, {1, 4, 4}, {1, 4, 3}, {0, 4, 3}, {0, 4, 4},
{0, 3, 4}, {1, 3, 4}, {1, 3, 3}, {0, 3, 3}, {0, 2, 3},
{0, 2, 4}, {0, 1, 4}, {0, 1, 3}, {0, 0, 3}, {0, 0, 4},
{1, 0, 4}, {1, 0, 3}, {2, 0, 3}, {2, 0, 4}, {3, 0, 4},
{3, 0, 3}, {3, 1, 3}, {3, 1, 2}, {3, 0, 2}, {4, 0, 2},
{4, 1, 2}, {4, 1, 3}, {4, 0, 3}, {4, 0, 4}, {4, 1, 4},
{3, 1, 4}, {3, 2, 4}, {2, 2, 4}, {2, 1, 4}, {1, 1, 4},
{1, 2, 4}, {1, 2, 3}, {1, 1, 3}, {1, 1, 2}, {0, 1, 2},
{0, 0, 2}, {1, 0, 2}, {1, 0, 1}, {0, 0, 1}, {0, 0, 0},
{1, 0, 0}, {1, 1, 0}, {1, 1, 1}, {2, 1, 1}, {2, 0, 1},
{2, 0, 2}, {2, 1, 2}, {2, 1, 3}, {2, 2, 3}, {2, 2, 2},
{2, 3, 2}, {2, 3, 1}, {2, 2, 1}, {2, 2, 0}, {2, 3, 0},
{1, 3, 0}, {1, 4, 0}, {0, 4, 0}, {0, 3, 0}, {0, 3, 1},
{1, 3, 1}, {1, 2, 1}, {1, 2, 0}, {0, 2, 0}, {0, 1, 0},
{0, 1, 1}, {0, 2, 1}, {0, 2, 2}, {1, 2, 2}, {1, 3, 2},
{0, 3, 2}, {0, 4, 2}, {0, 4, 1}, {1, 4, 1}, {1, 4, 2},
{2, 4, 2}, {2, 4, 1}, {3, 4, 1}, {3, 3, 1}, {3, 3, 2},
{3, 4, 2}, {4, 4, 2}, {4, 3, 2}, {4, 3, 1}, {4, 4, 1},
{4, 4, 0}, {4, 3, 0}, {3, 3, 0}, {3, 4, 0}, {2, 4, 0}
Or, more concisely, using base-5 notation:
|
50,
|
55,
|
80,
|
81,
|
76,
|
|
75,
|
100,
|
101,
|
106,
|
105,
|
|
110,
|
85,
|
86,
|
111,
|
112,
|
|
87,
|
88,
|
113,
|
114,
|
119,
|
|
118,
|
123,
|
124,
|
99,
|
98,
|
|
93,
|
94,
|
69,
|
68,
|
73,
|
|
74,
|
49,
|
48,
|
23,
|
24,
|
|
19,
|
44,
|
43,
|
18,
|
13,
|
|
14,
|
9,
|
8,
|
3,
|
4,
|
|
29,
|
28,
|
53,
|
54,
|
79,
|
|
78,
|
83,
|
82,
|
77,
|
102,
|
|
107,
|
108,
|
103,
|
104,
|
109,
|
|
84,
|
89,
|
64,
|
59,
|
34,
|
|
39,
|
38,
|
33,
|
32,
|
7,
|
|
2,
|
27,
|
26,
|
1,
|
0,
|
|
25,
|
30,
|
31,
|
56,
|
51,
|
|
52,
|
57,
|
58,
|
63,
|
62,
|
|
67,
|
66,
|
61,
|
60,
|
65,
|
|
40,
|
45,
|
20,
|
15,
|
16,
|
|
41,
|
36,
|
35,
|
10,
|
5,
|
|
6,
|
11,
|
12,
|
37,
|
42,
|
|
17,
|
22,
|
21,
|
46,
|
47,
|
|
72,
|
71,
|
96,
|
91,
|
92,
|
|
97,
|
122,
|
117,
|
116,
|
121,
|
|
120,
|
115,
|
90,
|
95,
|
70
|
Rob Pratt found an example of a full snake in the 7 × 7 × 7 case. It looks like this:
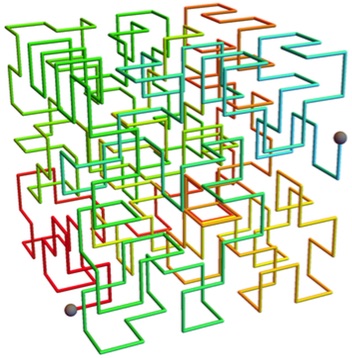
The sequence of points is
{{1, 3, 1}, {2, 3, 1}, {2, 3, 2}, {1, 3, 2}, {1, 3, 3}, {1, 4, 3}, {1, 4, 2},
{1, 5, 2}, {1, 5, 1}, {1, 4, 1}, {2, 4, 1}, {2, 5, 1}, {2, 5, 2}, {2, 6, 2},
{2, 6, 1}, {2, 7, 1}, {1, 7, 1}, {1, 6, 1}, {1, 6, 2}, {1, 7, 2}, {1, 7, 3},
{2, 7, 3}, {2, 7, 2}, {3, 7, 2}, {3, 6, 2}, {3, 6, 1}, {3, 7, 1}, {4, 7, 1},
{4, 6, 1}, {5, 6, 1}, {5, 7, 1}, {5, 7, 2}, {5, 6, 2}, {6, 6, 2}, {6, 7, 2},
{6, 7, 1}, {6, 6, 1}, {7, 6, 1}, {7, 7, 1}, {7, 7, 2}, {7, 6, 2}, {7, 6, 3},
{7, 7, 3}, {7, 7, 4}, {7, 6, 4}, {7, 6, 5}, {6, 6, 5}, {6, 7, 5}, {7, 7, 5},
{7, 7, 6}, {7, 6, 6}, {6, 6, 6}, {6, 7, 6}, {6, 7, 7}, {7, 7, 7}, {7, 6, 7},
{6, 6, 7}, {6, 5, 7}, {7, 5, 7}, {7, 4, 7}, {6, 4, 7}, {6, 4, 6}, {7, 4, 6},
{7, 5, 6}, {6, 5, 6}, {6, 5, 5}, {6, 4, 5}, {7, 4, 5}, {7, 5, 5}, {7, 5, 4},
{7, 4, 4}, {7, 4, 3}, {7, 5, 3}, {6, 5, 3}, {6, 5, 2}, {5, 5, 2}, {5, 5, 3},
{5, 4, 3}, {6, 4, 3}, {6, 3, 3}, {5, 3, 3}, {5, 2, 3}, {4, 2, 3}, {4, 3, 3},
{4, 3, 2}, {4, 4, 2}, {4, 4, 1}, {4, 3, 1}, {5, 3, 1}, {5, 3, 2}, {5, 2, 2},
{6, 2, 2}, {6, 2, 1}, {5, 2, 1}, {5, 1, 1}, {5, 1, 2}, {6, 1, 2}, {6, 1, 1},
{7, 1, 1}, {7, 2, 1}, {7, 2, 2}, {7, 1, 2}, {7, 1, 3}, {6, 1, 3}, {6, 1, 4},
{6, 2, 4}, {6, 2, 3}, {7, 2, 3}, {7, 3, 3}, {7, 3, 2}, {6, 3, 2}, {6, 3, 1},
{7, 3, 1}, {7, 4, 1}, {7, 4, 2}, {7, 5, 2}, {7, 5, 1}, {6, 5, 1}, {6, 4, 1},
{6, 4, 2}, {5, 4, 2}, {5, 4, 1}, {5, 5, 1}, {4, 5, 1}, {4, 5, 2}, {3, 5, 2},
{3, 5, 1}, {3, 4, 1}, {3, 4, 2}, {2, 4, 2}, {2, 4, 3}, {2, 3, 3}, {3, 3, 3},
{3, 4, 3}, {4, 4, 3}, {4, 5, 3}, {3, 5, 3}, {3, 6, 3}, {3, 6, 4}, {3, 5, 4},
{4, 5, 4}, {4, 4, 4}, {4, 4, 5}, {3, 4, 5}, {3, 5, 5}, {4, 5, 5}, {4, 5, 6},
{4, 4, 6}, {4, 4, 7}, {5, 4, 7}, {5, 5, 7}, {5, 5, 6}, {5, 4, 6}, {5, 4, 5},
{5, 5, 5}, {5, 5, 4}, {6, 5, 4}, {6, 4, 4}, {5, 4, 4}, {5, 3, 4}, {5, 3, 5},
{4, 3, 5}, {4, 3, 4}, {3, 3, 4}, {3, 4, 4}, {2, 4, 4}, {2, 4, 5}, {2, 5, 5},
{1, 5, 5}, {1, 4, 5}, {1, 4, 4}, {1, 5, 4}, {1, 5, 3}, {1, 6, 3}, {2, 6, 3},
{2, 5, 3}, {2, 5, 4}, {2, 6, 4}, {1, 6, 4}, {1, 7, 4}, {2, 7, 4}, {2, 7, 5},
{2, 6, 5}, {1, 6, 5}, {1, 7, 5}, {1, 7, 6}, {1, 6, 6}, {1, 6, 7}, {1, 7, 7},
{2, 7, 7}, {2, 6, 7}, {3, 6, 7}, {3, 7, 7}, {3, 7, 6}, {2, 7, 6}, {2, 6, 6},
{3, 6, 6}, {3, 6, 5}, {3, 7, 5}, {4, 7, 5}, {4, 6, 5}, {4, 6, 4}, {4, 7, 4},
{3, 7, 4}, {3, 7, 3}, {4, 7, 3}, {4, 7, 2}, {4, 6, 2}, {4, 6, 3}, {5, 6, 3},
{5, 7, 3}, {6, 7, 3}, {6, 6, 3}, {6, 6, 4}, {6, 7, 4}, {5, 7, 4}, {5, 6, 4},
{5, 6, 5}, {5, 7, 5}, {5, 7, 6}, {5, 6, 6}, {5, 6, 7}, {5, 7, 7}, {4, 7, 7},
{4, 7, 6}, {4, 6, 6}, {4, 6, 7}, {4, 5, 7}, {3, 5, 7}, {3, 4, 7}, {3, 4, 6},
{3, 5, 6}, {2, 5, 6}, {2, 5, 7}, {1, 5, 7}, {1, 5, 6}, {1, 4, 6}, {1, 4, 7},
{2, 4, 7}, {2, 4, 6}, {2, 3, 6}, {2, 3, 7}, {1, 3, 7}, {1, 3, 6}, {1, 2, 6},
{1, 2, 7}, {1, 1, 7}, {1, 1, 6}, {2, 1, 6}, {2, 1, 5}, {1, 1, 5}, {1, 1, 4},
{2, 1, 4}, {2, 2, 4}, {1, 2, 4}, {1, 2, 3}, {1, 1, 3}, {1, 1, 2}, {2, 1, 2},
{2, 1, 3}, {3, 1, 3}, {3, 2, 3}, {2, 2, 3}, {2, 2, 2}, {1, 2, 2}, {1, 2, 1},
{1, 1, 1}, {2, 1, 1}, {2, 2, 1}, {3, 2, 1}, {3, 3, 1}, {3, 3, 2}, {3, 2, 2},
{4, 2, 2}, {4, 2, 1}, {4, 1, 1}, {3, 1, 1}, {3, 1, 2}, {4, 1, 2}, {4, 1, 3},
{5, 1, 3}, {5, 1, 4}, {4, 1, 4}, {4, 2, 4}, {5, 2, 4}, {5, 2, 5}, {4, 2, 5},
{4, 1, 5}, {3, 1, 5}, {3, 1, 4}, {3, 2, 4}, {3, 2, 5}, {3, 3, 5}, {2, 3, 5},
{2, 3, 4}, {1, 3, 4}, {1, 3, 5}, {1, 2, 5}, {2, 2, 5}, {2, 2, 6}, {3, 2, 6},
{3, 1, 6}, {3, 1, 7}, {2, 1, 7}, {2, 2, 7}, {3, 2, 7}, {3, 3, 7}, {3, 3, 6},
{4, 3, 6}, {4, 3, 7}, {5, 3, 7}, {5, 3, 6}, {5, 2, 6}, {4, 2, 6}, {4, 2, 7},
{5, 2, 7}, {5, 1, 7}, {4, 1, 7}, {4, 1, 6}, {5, 1, 6}, {5, 1, 5}, {6, 1, 5},
{6, 1, 6}, {7, 1, 6}, {7, 1, 7}, {6, 1, 7}, {6, 2, 7}, {7, 2, 7}, {7, 3, 7},
{6, 3, 7}, {6, 3, 6}, {7, 3, 6}, {7, 2, 6}, {6, 2, 6}, {6, 2, 5}, {6, 3, 5},
{6, 3, 4}, {7, 3, 4}, {7, 3, 5}, {7, 2, 5}, {7, 2, 4}, {7, 1, 4}, {7, 1, 5}}
[Back to Problem 1206]
© Copyright 2015 Stan Wagon. Reproduced with permission.
|