Problem of the Week 1206
Cubic Snake
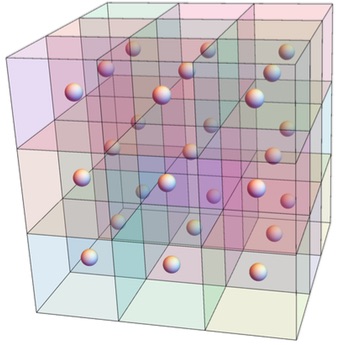
Consider a 3 × 3 × 3 cube, made up of 27 small cubes (cubies).
What is the longest possible length of a path that starts at the center of a cubie and proceeds to centers of adjacent cubies, never repeating a cubie, and, at every move, making a right-angled turn?
Here's a picture of the cube:
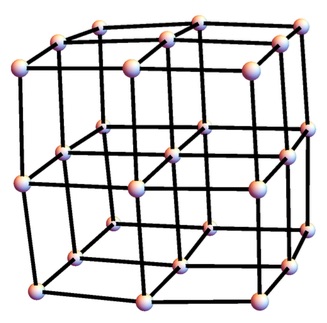
The problem is really about moves on the 3 × 3 × 3 grid graph, as pictured here:
Of more interest:
-
Same question for n × n × n made up of n³ cubies, where n = 4, 5,... . There is a right-angle path of length 4³ = 64 for the 4 × 4 × 4 case. But the question is open for n = 5 and larger. Note that the question is about partial Hamiltonian paths on the grid graph. For the 2 × 2 × 2 case, a right-angle turn is forced at any move, so any Hamiltonian path (or Hamiltonian cycle) works.
-
What about a 4-dimensional walk? What is the longest path for the 3 × 3 × 3 × 3 cube with 81 cubies?
Source: Terry Stickels, Larry Carter, Stan Wagon.
[View the solution]
|

