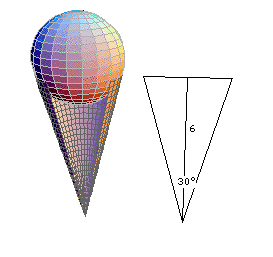Problem of the Week 1024

Hide the Calories

Imagine a right circular cone that is 6 inches high and has base angle of 30 degrees. Now place a sphere of ice cream inside and tangent to the cone.

What is the radius of the sphere that maximizes the volume of ice cream below the top of the cone?

Source: A nice new problem book with an emphasis on applications on modeling by Bill Briggs, called Ants, Bikes, and Clocks, and published by SIAM.

© Copyright 2005 Stan Wagon. Reproduced with permission.