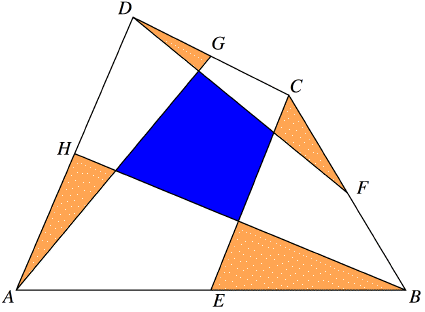
Problem of the Week 1144

A Crosscut Quadrilateral

Given a convex quadrilateral ABCD, let the midpoints of the sides be E for side AB, F for side BC, and so on. Then connect E to C, F to D, G to A, and H to B.

Prove that the area of the central quadrilateral equals the sum of the four shaded triangular areas.

Source: Rick Mabry, Crosscut convex quadrilaterals, Math. Mag., 84, Feb. 2011, 16-25.

© Copyright 2011 Stan Wagon. Reproduced with permission.