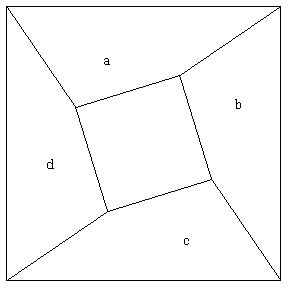
Problem of the Week 998

Square in a Square

A small square is placed inside a big square. The vertices of the small square are joined to a vertices of the large square in order, so as to divide the region between the squares into four quadrilaterals, with areas, in order, a, b, c, d. Prove that a+c=b+d.

Source: V. Dubrosky, Quantum July 1994 (spotted in Mathematical Chestnuts from Around the World" by Ross Honsberger, p. 119.

Here is a figure, and Mathematica code to generate it.

t = 17 Degree;
Show[Graphics[{Line[sq = {{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 0}}],
        Line[sq1 = sq /. {x_, y_} :> ({{Cos[t], -Sin[t]}, {Sin[
              t], Cos[t]}} . (.4({x, y} - {.5, .5}))) + {.5, .5}],
        Table[Line[{sq1[[i]], sq[[i]]}], {i, 4}],
        Text["a", {.37, .8}],
                        Text["b", {.85, .64}], Text["
                            c", {.66, .14}], Text["d", {.16, .42}] }], \
AspectRatio -> Automatic, TextStyle -> {FontFamily -> Times, FontSize -> 14}];

© Copyright 2003 Stan Wagon. Reproduced with permission.