Solution
This is quite a subtle problem, and I received plausible solutions from Michael Elgersma, Bob Bixler, Jim Tilley, and Jim Guilford.
For a detailed set of notes outlining all I know about this, including all my Mathematica code, download this PDF. For the notebook also, in case anyone wants to learn or play with the code, download the .nb file.
Here is a summary of how to get a rigorous solution, with ideas due to David Finn.
Find a parametric function f0(t) = (x(t), y(t)) that goes from (0, 0) to (1, 0) and is infinitely flat (all derivatives are 0) at both ends. Simplest is f0 = (t, e^(-1/(t(1 − t))).
Use f0 as the path of the rear wheel and use it to generate, by tangency because the unit-length tangent to the rear track always points to the front track, a path for the front wheel. To be precise, if f0 is as given, then f1 = f0 + df0 / ||df0|| gives f1, which is the next segment of track. Here, df0 refers to the (vector) derivative of f0, and we divide by its length since we want a unit vector.
Now, f1 is not too complicated, and it too is infinitely flat at its ends. So one can carry forward to f2, f3, ... f_n , ..., though things get quite complicated as n rises.
The image of this bike = unicycle path is interesting and amusing, and I encourage you to view the diagrams of several iterations of this in my notes, e.g.,
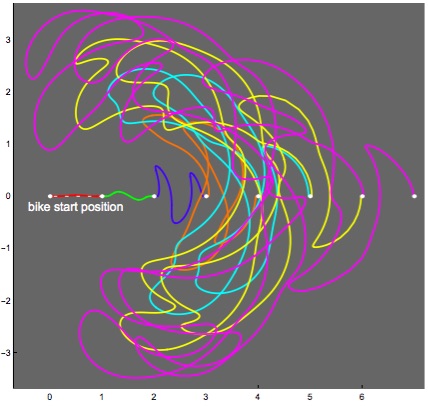
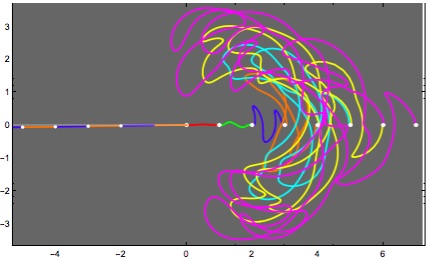
Note that f, though infinitely differentiable, is not analytic. This is the only true application of a nonanalytic function that I know!
Questions:
-
Can there be a half-infinite nonstraight bike = unicycle path that is analytic?
-
Can there be a half-infinite nonstraight bike = unicycle path that never crosses itself, perhaps spiralling outwards in some controlled way?
One can also run the process backwards, and treat f0 as the front track. The rear track is then obtainable by (numerical) solution to a fairly simple differential equation. This was Jim Guilford's approach. One observes that such reverse tracks become asymptotic to straight lines, and Michael Elgersma has a proof that this is always the case. It is related to this observation by Serge Tabachnikov: The forward (tangent) operation always increases length; therefore the reverse (differential equation) decreases length.
Relevant papers for more on this fascinating subject are:
D. Finn, Can a bicycle create a unicycle track? College Math. Journal, 33:4 (Sept. 2002) 283-292.
R. L. Foote, M. Levi, S. Tabachnikov, Tractrices, bicycle tire tracks, hatchet planimeters, and a 100-year-old conjecture, Amer. Math. Monthly 120:3 (2013) 199-216.
Mark Levi and Serge Tabachnikov, Hatchet Planimeter, Menzin's Conjecture, and Oscillation of Unicycle Tracks, On bicycle tire tracks geometry, hatchet planimeter, Menzin's conjecture, and oscillation of unicycle tracks, Experimental Mathematics 18:2 (2009) 173-186.
Gil Bor, Mark Levi, Ron Perline, and Sergei Tabachnikov, Tire tracks and integrable curve evolution, preprint, July 2017.
[Back to Problem 1248]
© Copyright 2017 Stan Wagon. Reproduced with permission.