Solution
The minimal possible sum is 37294, as found by F. Barrera and as proved optimal by Gordon Royle.
Using these ten numbers as the labels gives the optimum:
2494, 3913, 3055, 2679, 6061,3034, 3689, 4255, 3813, 4301
These sums to 37294.
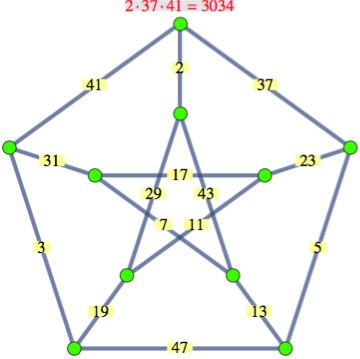
Each of these is a product of three primes, thus: {2, 29, 43}, {7, 13, 43}, {5, 13, 47}, {3, 19, 47}, {11, 19, 29}, {2, 37, 41}, {7, 17, 31}, {5, 23, 37}, {3, 31, 41}, {11, 17, 23}.
One wonders if asking for the same thing but using the indexes of the primes, rather than the primes themselves, would lead to a different minimum configuration. That is, the solution above would become
{1, 10, 14}, {4, 6, 14}, {3, 6, 15}, {2, 8, 15}, {5, 8, 10}, {1, 12, 13}, {4, 7, 11}, {3, 9, 12}, {2, 11, 13}, {5, 7, 9}
Therefore, we have {140, 336, 270, 240, 400, 156, 308, 324, 286, 315}, with total 2775. This would avoid the extra spacing one gets as the primes grow. And of course there is the question, probably very difficult and so perhaps suitable as an investigation into combinatorial optimization, of studying this problem on any graph.
The best way to look at the given problem is to use an assignment of the first 15 prime numbers, from 2 to 47, to the 15 edges. Then if p, q, and r are assigned to the three edges from vertex V, the label p q r is given to V. Naively, there are 15! ways to make this assignment, but various tricks can be used to reduce the search. Gordon Royle, using the MINION language, proved that the assignment given above is optimal; it looks like this:
Royle's method is tersely described at a recent MathOverflow thread.
But it is also possible to use brute force: assign 2 to one of the edges and then look at the 14! ways of assigning the other primes. That was done by Jim Guilford, who therefore has also proved that the optimum is 37294.
Various ad hoc methods were used by the others, e.g., Leone, who wrote, "My approach was to randomly assign the prime factors, then see how much the sum could be improved by swapping them. In about 14% of the 1000 cases I looked at, it could be improved down to 37294, but never further."
Many readers solved the problem of getting a sum under 100,000, and a few found the optimum of 37294. Those finding 37294 are Al Zimmermann, Jim Tilley, Mark Rickert, Ken Leone, Japheth Wood, Jim Guilford, Ken Duisenberg, and Michael Elgersma.