Problem of the Week 1236

A Shrinking Random Walk

Solution

Quite a few incorrect solutions were received. I count as correct solutions that said "it is clear" that the points are uniformly distributed along the line segment. But this does need proof, which I include below. After all, the integral is a continuous object over the whole segment, so one must pass to the limit one way or another.

Correct solutions (on first try) were submitted by Joseph DeVincentis, James Guilford, John Guilford, Patrick Fitzsimmons, Alberto Monteiro, Robert Silber, Ken Leone, and John Snyder.

Solution: At the walk's end, the x and y coordinates sum to 2√2, so the point is on L, the line segment connecting (0, 2√2) to (2√2, 0). The points are uniformly distributed on L (proof below) and so the expected distance is the integral of (1/2√2) √[x² + (2√2 - x)²] from 0 to 2 √2. This is √2 + ArcSinh[1], or √2 + Ln[1 + √2], or 2.29559... .

John Snyder gets extra credit for discovering that the answer is exactly the "universal parabolic constant"! This constant, P = 2.29558..., is the parabolic analog of pi, the ratio of the circumference of a semicircle to its radius. For those unfamiliar with this constant, see its entry in MathWorld and decimal expansion in the On-Line Encyclopedia of Integer Sequences.

He discovered this by entering 2.2955871 into Wolfram|Alpha; the output identifies this as being close to the universal parabolic constant. With this hint, it is easy to see that they are in fact identical.

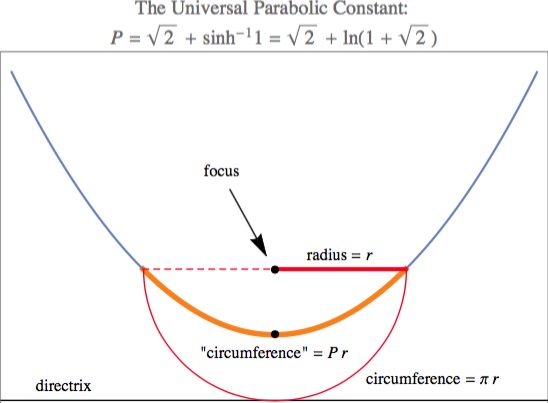
Details: For any parabola, the ratio of its "circumference" to its "radius" is

P = Ln( 1 + √2 ) + √2 = √2 + ArcSinh[1] = 2.29558...

Here, the "radius" is the horizontal (i.e., perpendicular to the axis of the parabola) distance from the focus to the parabola (this is the "semilatus rectum"). The "circumference" is the arc length of the parabolic segment lying below the focus (below relative to the axis; cut off by the latus rectum). The radius is also the distance from the focus to the directrix, as in this diagram:

The exact value of P above arises from a standard arc length integral. Further, P = the average distance of a point on a square of side-length 2√2 to its center. This is not a coincidence. Both integrals — the arc length for the parabola y = x²/2 (radius is 1 in this case) and the average distance for the square of side-length 2 — are

In both cases, the integrand arises directly from a (1, x, √[1 + x²]) right triangle.

Back to our problem: The answer to the random walk problem posed is P. But we need a proof of uniformity. View the flip sequence F as 1s and 0s, where 1 denotes a horizontal move, and then view this as a base-two number R in [0, 2]; then R is the x-coordinate of the limiting point. A rational interval of the form J = [a/2ⁿ, b/2ⁿ) has (b − a)/2^{(n + 1)} as its length-ratio-to-2. This quantity equals the probability that F begins with an n + 1-sequence of bits that is lexicographically between the binary forms of a and (strictly) b. Because the set of numbers that have duplicate binary representations is countable and so has probability 0 of occurring, this is the same as the probability that R lies in interval J.

For example, the interval [1/4, 3/2) has length-ratio-to-2 being 5/8, and x lies in this interval if the flip sequence F starts with 001, 010, 011, 100, or 101, the probability of which is 5/8. The dyadic rationals are dense, so this extends to all intervals by limits and proves that the distribution of x is uniform w.r.t. the product probability on the set of all sequences. This implies the same for pairs (x, y) on L, because y is a linear function of x.

[Back to Problem 1236]

© Copyright 2017 Stan Wagon. Reproduced with permission.