Solution
I received the same mod-7 solution from several of you: John Guilford, Jim Guilford, Joseph DeVincentis, Mark Rickert, Hugh Thomas, Patrick LoPresti, Stanley Rabinowitz, Stephen Morris. The protocol is this:
Alice: "The mod-7 sum of my cards is S."
Bob: "Eve's card is E."
(Bob could also say: "The mod-7 sum of my cards is T."
This is the same as:
Alice: "I am holding one of {1, 2, 4}, {1, 6, 7}, {2, 5, 7}, {3, 4, 7}, {3, 5, 6}.
Bob: "Eve's card is E."
More details below, including the proof that it works, which was rarely provided. But first, note that the "knowing truth" assumption is critical; and that the problem falls apart without that.
This problem was used in a Russian Olympiad, and some students submitted this solution:
Suppose the deal is A = 123, B = 456, E = 7.
Alice: "I am holding 123 or you are holding 123."
Bob: "I am holding 456 or you are holding 456."
Now upon hearing the two statements, Alice and Bob know all the cards. And the statements are both true. But what does Eve learn? This depends strongly on the assumptions.
If the assumptions are only that the statements made must be true, then Eve cannot know that Alice knows her statement is true. Eve knows only that the statements are true. So Eve learns no card's position and this must be considered a valid solution. Hence the students in the Olympiad were given full credit (to the chagrin of the graders).
But if the assumptions are as in Problem 1226 — each statement must be known to be true — then Eve can reason: "The only way Alice can know her statement is true is if Alice holds 123. Same for Bob. So now I know where all the cards are!" And therefore the solution is NOT valid.
To highlight the difference, consider the case of three cards, with Alice getting card 1 and Bob getting card 2.
The following solution works in the "true, but not known true" case:
Alice: "One of us has 1."
Bob: "One of us has 2."
These are true, but Eve cannot be certain of anything new.
But under the proper formulation, this is not a solution because Eve would know Alice had 1. Moreover, under the proper formulation, there is no solution. For Alice's statements can be only
-
My card is 1.
-
My card is 1 or 2.
-
My card is 1 or 3.
-
My card is 1 or 2 or 3.
Statement (1) fails, as it tells Eve everything. Statement (4) fails, as it conveys nothing. Statement (2) works. Statement (3) fails, since Bob learns nothing. But Alice, not knowing Bob's card, cannot know which of (2) or (3) to state.
I believe also there is no solution for n = 5, with a 2, 2, 1, deal, but have not checked all possibilities.
So this is all very nice, since so often this type of knowledge problem fails to state exactly what the assumptions are. For a different view of the main issue, see the short note about this problem in The Mathematical Intelligencer (Dec. 2001, 23:1, 41-42).
Back to the original problem. A full solution must include a proof that the protocol works. Here is a proof by Hugh Thomas.
Since Bob has to be able to deduce Eve's card based on what Alice says, he may as well just announce Eve's card. Clearly this gives Eve no information, and tells Alice what she needs. My proposal for what Alice should announce is the sum of her cards mod 7. This is obviously sufficient: Bob can sum up his cards mod 7 and he knows that all 7 cards add up to zero, so from this he can deduce Eve's card.
I claim that Eve doesn't learn who has any card other than hers. This is a bit tricky to verify. Without loss of generality, we can subtract an equal amount (mod 7) to the label of each card so that Eve's card is 7. (If you prefer, you can think of Eve as carrying out this subtraction herself. The point is that she knows the effect of this subtraction on what Alice announces, so if Eve had a 1 and Alice announced 5, that is the same as Eve having a 7 and Alice announcing 2.) For each of the seven possibilities that Alice can announce, we have to check that there is no card that Eve can deduce is in Alice's hand or in Bob's hand.
If Alice's sum is zero, so is Bob's, so Eve certainly doesn't know which of their two hands is which.
By symmetry (4, 5, 6 being negatives of 3, 2, 1), we are left with checking the sums 1, 2, and 3 mod 7.
-
Alice's hand could be 456, 125, 134
-
Alice's hand could be 234, 135, 126
-
Alice's hand could be 136, 145, 235.
(These lists are not necessarily exhaustive.)
In each case, my three possibilities include all 6 cards other than Eve's, so Eve doesn't know any of Bob's cards, and the three possibilties have no triple intersection, so Eve doesn't know any of Alice's cards.
Questions such as these appear to be connected to the theory of combinatorial designs. The Fano plane appears to be relevant to the case posed. For example, a solution is for Alice to say: "I have one of 123, 145, 167, 246, 257, 347, 356." These are the lines in Fano plane, which is connected to the 3-bit Gray code. Here is a diagram:
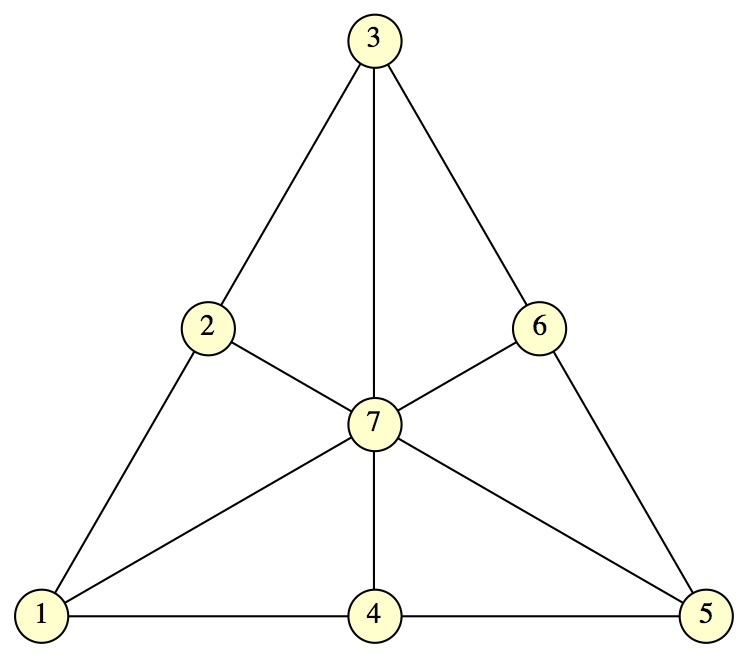
A natural extension for PoW #1226 is to resolve the general case where Alice and Bob get n cards and Eve gets 1. I do not know the answer.
[Back to Problem 1226]
© Copyright 2016 Stan Wagon. Reproduced with permission.