Problem of the Week 1210

Drink Me

Solution

This asked for a "shrinkable" region in the plane. Several solutions were received, with some further investigating extensions to three dimensions. All solutions found were identical to, or small variations on, the one discovered by proposer Dan Asimov many years ago:

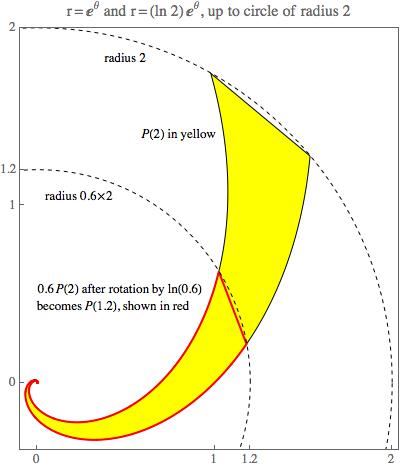
Consider the region P(q) formed by the two arms of the logarithmic spirals given, in polar coordinates, by r = e^θ and r = (ln 2) e^θ, with each extended until it strikes the circle of radius q. Then P(2) solves the problem, since any k P(2) (where 0 < k < 1) is, after rotation by ln k, equal to P(k 2), which is contained in P(2).

Here is a diagram of this shrinkable region P(2):

[Back to Problem 1210]

© Copyright 2015 Stan Wagon. Reproduced with permission.