Solution
Shoesmith labelings do not exist for W(4k). A short proof (as well as related results and questions) is in Ian Anderson, "Magic polygons and Shoesmith labellings," Bull. ICA 74 (2015)103-112.
The problem asked for a Shoesmith labeling of W(6), which looks like this:
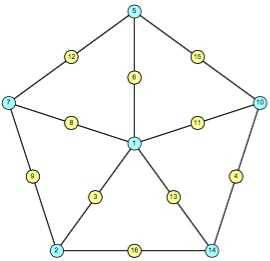
This was found by Joseph DeVincentis, John Snyder, Stephen Meskin, Robert Israel, and Rob Pratt. Note that the labels are 1 through 16, and the label of each edge is the sum or positive difference of the labels of its ends.
Rob Pratt (SAS) did an extensive computation using ILP (integer-linear programming) and found that these labelings exist for W(n) for all n up to 19 (except n = 4k, of course). So the conjecture is that they exist for all W(n) when n is not a multiple
of 4.
Joseph DeVincentis had a heuristic idea that allowed him to go up to W(10) by hand, which was more than was done in the source paper.
[Back to Problem 1209]
© Copyright 2015 Stan Wagon. Reproduced with permission.