Solution
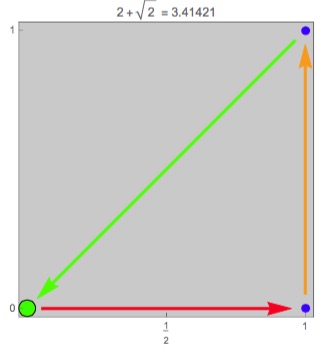
Several readers found the longest known 6-cycle:
{(1/2, 0), (1, 0), (1/2, √3/2), (0, 1), (0, 0), (1, 1), (1/2, 0), (1/2, 0)}
Its length is 5.54989... Here is an image:
Here are the longest known ones for some other cases:
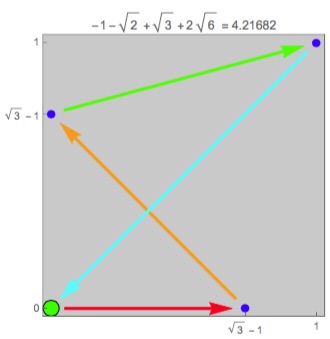
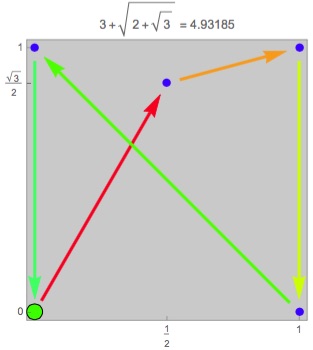
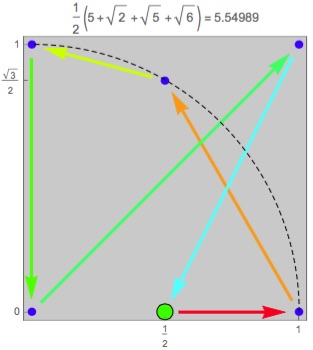
Many more examples of the best known are at this web page set up by Erich Friedman.
The best cycle for the posed case was found by Robert Israel, Al Zimmermann, Witold Jarnicki, and Rob Pratt. Several others found the same point set, but started the cycle at the origin, which is not as good as the start point above. Note that in the literature this algorithm is sometimes called the "Nearest Neighbor" algorithm for the traveling salesman problem, with "Greedy" reserved for the algorithm that, at each step, chooses the shortest possible edge among the legal edges currently remaining.
Pratt found this paper, which presents a general upper bound for this problem:
L. Tassiulas, Worst Case Length of the Nearest Neighbor Tours for the Euclidean Traveling Salesman Problem, SIAM J. Discrete Math., 10 (1997) 171-179
[Back to Problem 1207]
© Copyright 2015 Stan Wagon. Reproduced with permission.