Solution
Several of you found the 11-step solution (i.e., 11 pouring
steps) to the problem as posed:
|
(12 0 0)
|
→
|
(5 7 0)
|
→
|
(5 1 6)
|
→
|
(11 1 0)
|
→
|
(11 0 1)
|
→
|
(4 7 1)
|
|
|
|
→
|
(4 2 6)
|
→
|
(10 2 0)
|
→
|
(10 0 2)
|
→
|
(3 7 2)
|
→
|
(3 3 6)
|
→
|
(9 3 0)
|
I had thought this was the hardest instance with capacities (A, B, C) = (12, 7, 6), but in fact a harder one is to start with (6, 0, 6) and obtain 9 in the first jug. That is one step longer.
I had also thought that the family (4k, 2k + 1, 2k) yielded the most difficult problems in general, but that is false. The family that I used was: capacities (4k, 2k + 1, 2k), start = (2k, 0, 2k), finish = (3k, k, 0) requires A steps.
But there are harder ones. The case of capacities (2k + 1, 2k + 1, 2), start = (0, 2k + 1, 2), finish = (1, 2k + 1, 1) requires A + 1 steps.
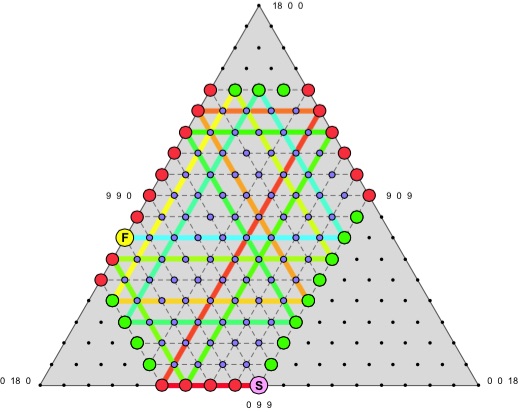
And there is more. Witold Jarnicki (Krakow) found that when k ≥ 2, capacities (6k + 2, 6k + 1, 4k + 1), start = (0, 4k + 1, 4k + 1), finish = (3k + 1, 5k + 1, 0) requires 8k, or (4/3)(A − 2) steps.
When k = 2, this means (14, 13, 9) has a case requiring 16 steps.
These are not proved in general; possibly they are not hard using the graph theory setup I will describe below. Are there any cases that are worse than (4/3)(A − 2)? I see also that this next case requires 20 (= A + 3) steps (going from (0, 11, 11) to (3, 8, 11) when capacities are (17, 16, 11).
Some of you have been investigating the problem in detail. Rob Pratt and Witold Jarnicki have carried out extensive computations, and Stephen Morris and Piotr Zielinski have investigated possible proofs of bounds on path-length. When more details become clear, I will post them. I do not know of any other published work on this aspect of pouring problems.
The correct way to study the problem combines graph theory and billiards. A capacity set (A, B, C) can be viewed via barycentric coordinates (also called trilinear coordinates) as a graph using discrete vertices in an equilateral triangle.
Any state (a, b, c) with total water a + b + c = T gives the point (a, b, c).(u, v, w)/T, where (u, v, w) are the vertices of an equilateral triangle. We form graph G by considering legal states (the capacities are not exceeded) to be the vertices, and with a directed edge from one state to another if one can get from one to the other by pouring.
This diagram shows the solution:
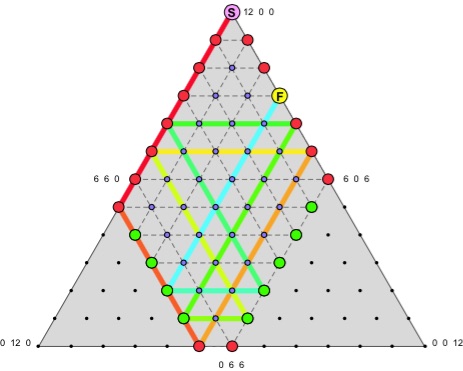
And this diagram shows the harder (14, 13, 9) case:
Useful facts:
-
Any edge of G terminates in a state having at least one empty jug, or at
least one full jug. These are on the border of the polygon of legal states.
-
The shortest path in G from one state to another gives the shortest way
to reach the target by the pouring rules.
-
Any edge of G follows one of the three directions parallel to a side of
the triangle, and the edge goes to the last possible point (i.e., going
farther would leave the polygon).
-
The paths of G repeatedly reflect in the sides as a billiard path would.
So setting up the graph and using a fast ShortestPath algorithm allows one to solve any such problem. I will soon post a demo at the Wolfram demo site that allows the user to select the problem and shows the optimal solution in the graph.
Piotr Zeilinski has a sketch of a proof that, for jugs of capacities A ≥ B ≥ C, and with total water in the initial state being A, the longest path in the graph — i.e., the longest number of steps to get from the initial state to a reachable final state — is A + 1. Experiments indicate that the only case that requires A + 1 steps is when the capacities are (A, A, 2) with A odd, the initial state is (A, 0, 0) and the final state is (A − 1, 0, 1).
Download Zeilinski's notes here: s1204.pdf
I believe there are still more details to fill in; but as far as I know, this is the first indication of a theorem that gives an upper bound in the whole area of such jug problems with 3 or more jugs (I think the 2-jug case is related to the Euclidean algorithm).
MathWorld discusses this problem, as does Alexander Bogomolny.
Here's a demo for the two-jug problem: http://demonstrations.wolfram.com/WaterPouringProblem
[Back to Problem 1204]
© Copyright 2015 Stan Wagon. Reproduced with permission.