Solution
The minimal solution was found and proved minimal by Adam Sztrebonski (Wolfram Research, Inc.), Joseph DeVincentis, and Al Zimmerman. The second best solution was found by one reader.
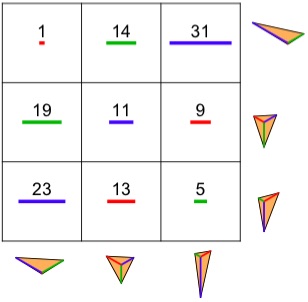
This semi-magic Wye square is the smallest solution in integers:
1 14 31
19 11 9
23 13 5
What happens here is that the three numbers in any row and column yield a triangle when the three numbers are viewed as rays emanating from a common point, with 120° between the rays. The areas of the resulting six triangles are all the same.
So if a triple is (a, b, c) and we ignore a leading constant, then the area of the triangle (use 1/2 a b sin(θ) area formula) is
a c + b c + a b
This last expression is the same for all six triples. One can prove minimality of the solution shown by an exhaustive search, which does not take too long. That was done by DeVincentis and Zimmerman.
Adam Sztrebonski did it using quite different algebraic techniques, as pictured below:
The above is semi-magic. There are also fully magic solutions where, in addition, the two diagonals yield triangles of the same area. The numbers are much larger. Sztrebonski found this one:
4158 5544 12474
18480 6930 630
2970 8470 10395
It is a little nicer in this rational form:
3 4 9
40/3 5 5/11
15/7 55/9 15/2
[Back to Problem 1203]
© Copyright 2015 Stan Wagon. Reproduced with permission.