Problem of the Week 1202

Magic Triangles

Solution

I received solutions, with proof of optimality, from Rob Pratt, Witold Jarnicki, and Joseph DeVincentis. Three others found the solution, but without proof of minimality. One reader found an example that was not minimal.

To get the minimal solution, start with the classic Lo Shu — the smallest magic square using distinct positive integers:

   4   9   2
   3   5   7
   8   1   6

Here, each row, column, and diagonal sums to 15.

Add 4 to each entry to get

   8   13   6
   7    9  11
   12   5  10

Now all eight triples are nondegenerate triangles, and each of the eight perimeters is 15 + 12 = 27. Here's a nice picture of the triangles and magic square:

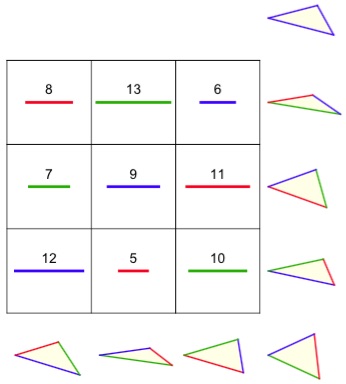
This is the smallest possible solution.

Here is Witold Jarnicki's very slick proof of minimality.

Let M ≥ 9 be the biggest of the 9 numbers; let P be the common perimeter; let S be the sum of all 9 numbers. A triangle containing M is (a, b, M) where a + b is at least M + 1, so P ≥ 2M + 1. So we have

3(2M + 1) ≤ 3P = S ≤ (M − 8) (M − 7) ... M = 9M − 36.

But 3(2M + 1) ≤ 9M − 36 is the same as 2M + 1 ≤ 3M − 12 or M ≥ 13; therefore, P cannot be smaller than 27.

Some work by Witold Jarnicki (Krakow, Poland) and Adam Sztrebonski (Champaign, Illinois) resolved the open question. They showed that there does not exist a 3 × 3 square of distinct positive real numbers so that the six nondegenerate triangles one gets from the rows and columns all have the same area.

[Back to Problem 1202]

© Copyright 2015 Stan Wagon. Reproduced with permission.