Solution
I received several solutions. The easiest way is to work out the coordinates of X and take the limit.
Sam Vandervelde found a geometric approach somewhat similar to the one I will present here. Just before posting the problem, I received beautiful geometric solutions from John Duncan and John Webb, who saw it in a publication of mine. Here is a composite of their solution:
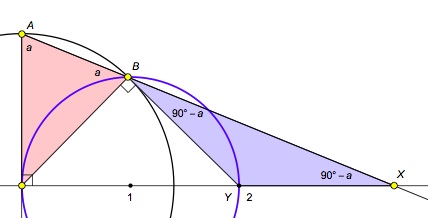
Argue as follows: The leftmost pink triangle is isosceles (two radii), so the base angles a are equal. But then the upper left angle of the blue triangle is 90 − a, which is the same as the angle at X (large right triangle). So the blue triangle is isosceles and BY = YX. As the black circle shrinks, the length of BY approaches 2, and so the length of BX approaches 2 + 2 = 4. John Duncan suggests that this proof is in THE BOOK.
Jerry Grossman (Oakland U.) observes that computations support the generalization: If the circle centered at the origin is replaced by the ellipse centered at the origin with positive y-intercept r and positive x-intercept k*r, then the line hits the x-axis at a point that approaches (2k)² as r goes to 0. I did some quick algebraic work on the equations and it appears that a proof by coordinate geometry and computer algebra is simple.
[Back to Problem 1192]
© Copyright 2014 Stan Wagon. Reproduced with permission.