Solution Notes
I received many correct solutions to the problem as posted, though only a few carried it farther to give more information.
For the given problem one can see the inequality is FALSE for large numbers. As Joseph DeVincentis wrote:
"Consider the numbers from 0 to 10^n - 1, written as n-digit numbers with leading zeroes. These 10^n numbers include all possible strings of n decimal digits, and each digit appears in each position equally often. This means 1/10 of all the digits are 1. Therefore a(10^n - 1) = n/10 * 10^n = n 10^(n-1). So we have a(9)=1, a(99)=20, a(999)=3 100, a(9999)=4 1000, and so on: a(10^n-1)=n 10^(n-1). Therefore the inequality fails at n=10 (i.e., numbers up to 10^10 -1), since a(10^10-1) = 10^10."
A little more work shows that a(n) < n fails at n = 200000, and working backwards from there one finds it fails at 199981, which is in fact the first failure. It is known (see OEIS references) that there are 84 numbers (counting 0) for which a(n)=n: the full list is
{0,1,199981,199982,199983,199984,199985,199986,199987,199988,199989,
199990,200000,200001,1599981,1599982,1599983,1599984,1599985,1599986,
1599987,1599988,1599989,1599990,2600000,2600001,13199998,35000000,
35000001,35199981,35199982,35199983,35199984,35199985,35199986,
35199987,35199988,35199989,35199990,35200000,35200001,117463825,
500000000,500000001,500199981,500199982,500199983,500199984,
500199985,500199986,500199987,500199988,500199989,500199990,
500200000,500200001,501599981,501599982,501599983,501599984,
501599985,501599986,501599987,501599988,501599989,501599990,
502600000,502600001,513199998,535000000,535000001,535199981,
535199982,535199983,535199984,535199985,535199986,535199987,
535199988,535199989,535199990,535200000,535200001,1111111110}
and it is known that, beyond the last element of this list, a(n) > n.
I made a logarithmic plot that nicely shows the whole story up to 1.2 billion. You can see it at
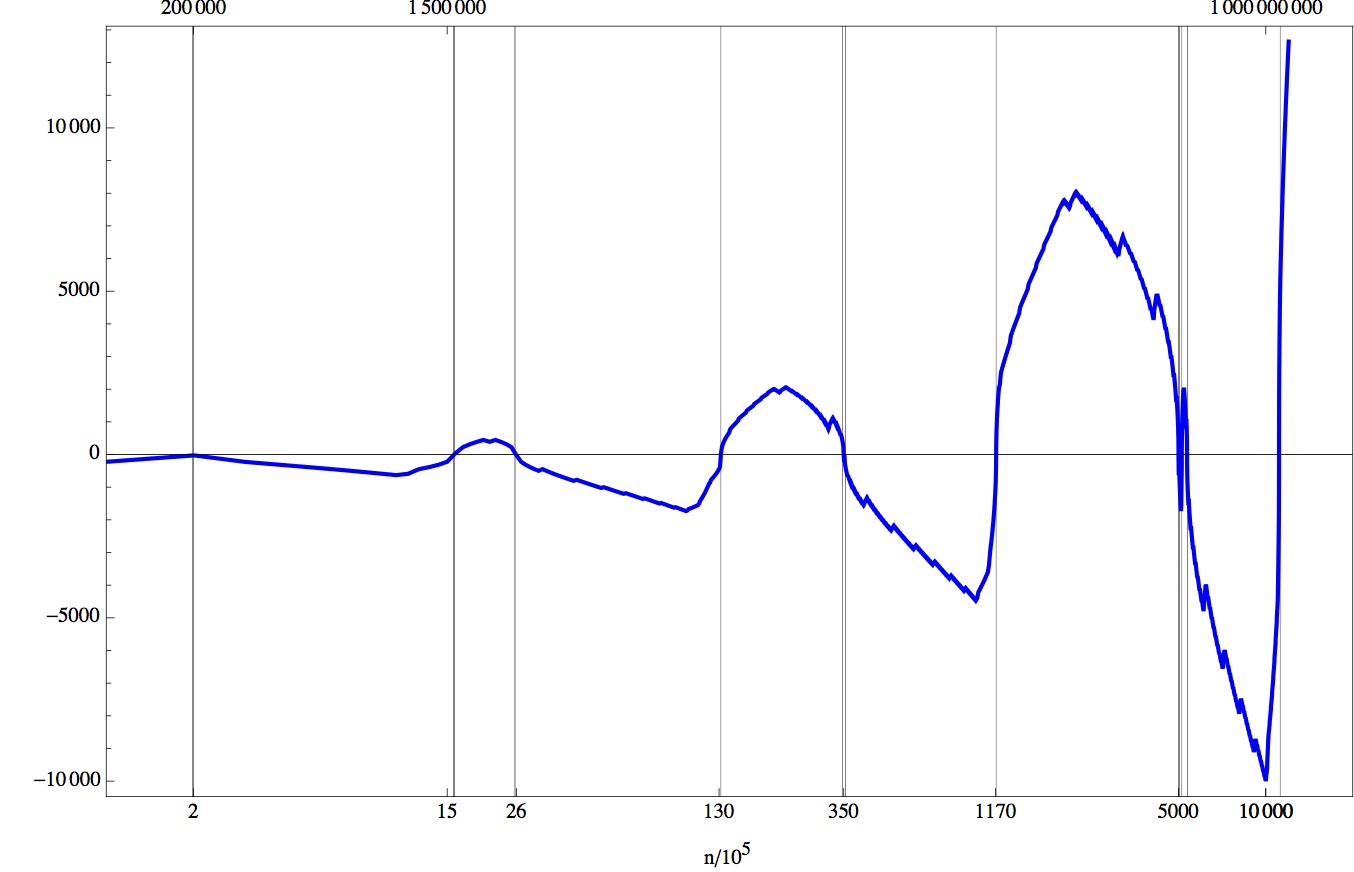
click to view larger image
David Broadhurst (London) presented a very efficient recursive method for
calculating a(n) when n is very large. In words,
"My recursion is suited to much larger numbers. Let n have k digits and let f be the leftmost digit of n. Let t = 10^(k-1).
Then r = n - f * t, is the number obtained by removing the leftmost digit of n. I use the neat recursion
a(n) = a(r) + f * (k-1) * t/10 + If[ f == 1, r+1, t]
which is also useful for proving inequalities like a(n) > n, for n > 10^10, and identities like a(10*(10^k-1)/9) = (k+1)*(10^k-1)/9 which gives the last case of a(n)=n, at k=9."
In short, he worked out an efficient method of getting a(xyz....w) from a(yz....w). Here is complete Mathematica code for his method, where I worked iteratively rather than recursively.
a[n_] := ( L = Reverse[IntegerDigits[n]];
m = c = 0; p = 1;
Do[ f = L[[k]]; If[f != 0, c += f (k-1) p/10 + If[ f == 1,
m+1, p]; m += p f];
p *= 10, {k, Length[L]}];
c )
This method takes only a millisecond to work out a(1234567891011...9899100),
where the argument is itself a 192-digit Champernowne-like number; it is:
238984908864235740859260908235500441154942960881130455997101924252215
038873806342168754167529856214630747841644689541638196061214120603191
0988262380977410894561367166203407412679926496883931741
References:
https://oeis.org/A094798
https://oeis.org/A014778
* The problem was apparently used on a Google Labs Aptitude Test. See Problem #17 at http://mathworld.wolfram.com/news/2004-10-13/google/
[Back to Problem 1181]
© Copyright 2014 Stan Wagon. Reproduced with permission.