Solution Notes
Problem 1180 was solved by Joseph DeVincentis, Sun Gonglei, Ding Yuting, Stephen Meskin, Stephen Morris, Zhu Jiaxin, Xie Jia, Junhao Liu, Stella Tang, Damon Chai. One incorrect solution was received. Thetwo counts are the same. Some very long solutions were received, but really it is very short. The result holds for any power of 10 instead of 10^1180. As S. Morris wrote:
For any digit in the set of numbers up to 10^(n-1) insert a zero immediately afterwards to create a larger number. Associate the digit with this zero. This process is reversible and a one-to-one mapping, proving that the counts are equal. Some care is needed, since the mapping is from "digits" to "zeroes". So for example, 56 yields 560 and 506. But 100 yields 1000 in three different ways. The point is that the mapping is bijective between the digits of 100 (three) and the zeroes of 1000 (three).
Here is an alternate view (essentially the same thing) that is just about as short, by J. DeVincentis. Consider D-digit numbers. In each position other than the first, when that digit is 0, removing it leaves a D-1 digit number. All D-1 digit numbers arise in this way, and each one arises D-1 times, for the possible positions of the removed 0. Thus:
(D-1) (number of D-1 digit numbers) = number of 0s in D-digit numbers.
But the left side is the number of digits in the D-1 digit numbers, proving the claimed equality for all D-digit numbers. Do this for every D up to n, yielding the result for all the numbers from 1 to 10^n - 1. The problem includes 10^n, but 10^n has as many zeroes as digits in 10^(n -1), so the relation holds for numbers in the interval [1, 10^n].
It is not hard to show that the number of digits in the sequence 1,2,3,...,10^n is given by n(10^n+1) - 10 ( 10^(n-1)-1)/9
For example, if n is 14, one subtracts:
1400000000000014
- 11111111111110
Ed Barbeau (U. of Toronto) writes that he knew of this problem for at least 30 years, but is unsure of the exact source. It appears as Problem 134 in "Which Way Did the Bicycle Go?" by Konhauser, Velleman, and Wagon. See also https://oeis.org/A072290.
Here is a stronger version that I have not completely analyzed. It might not be terribly interesting, but it seems clear that there is a simple characterization of the "good" pairs (i,j). If someone cares to work it out, I will post. Call a pair (i, j) "good" if the number of digits from 1 to i equals the number of 0s in the numbers from 1 to j. So Problem 1180 shows that any pair (10^n, 10 10^n) is good. Characterize the set of good pairs. I computed several thousand, and graphs of the results are posted at:
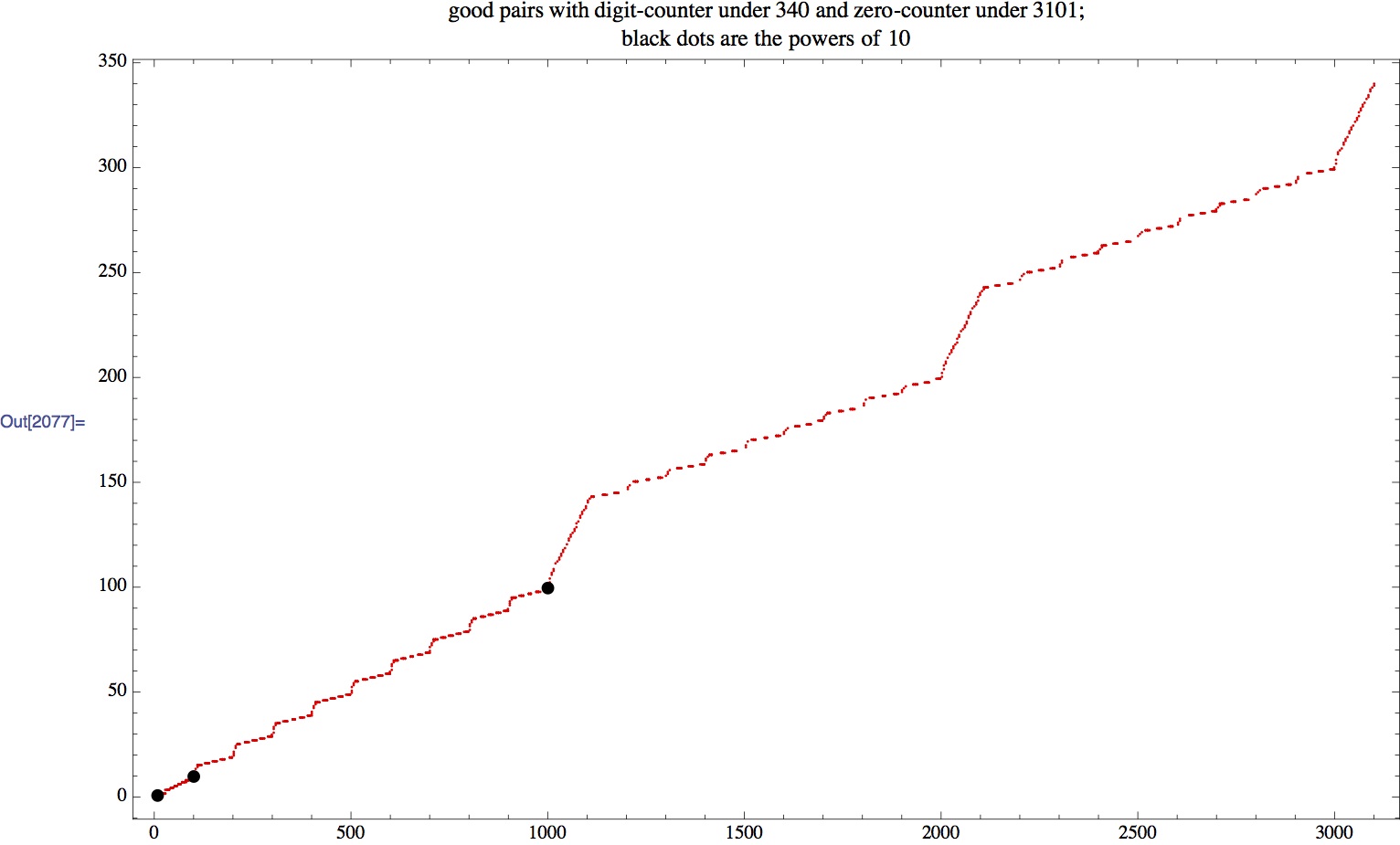
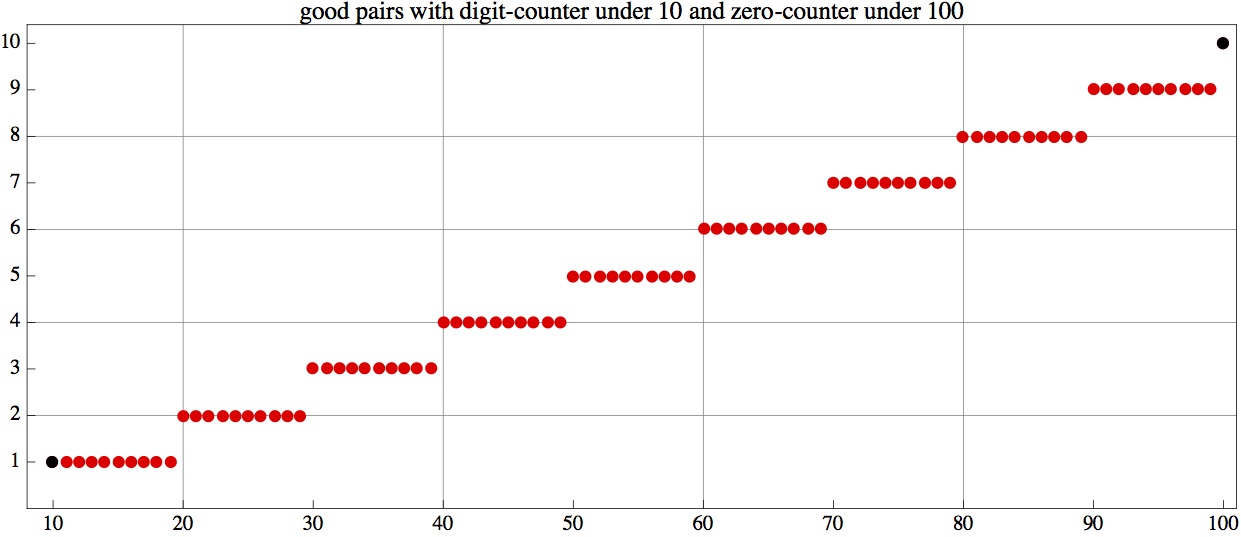
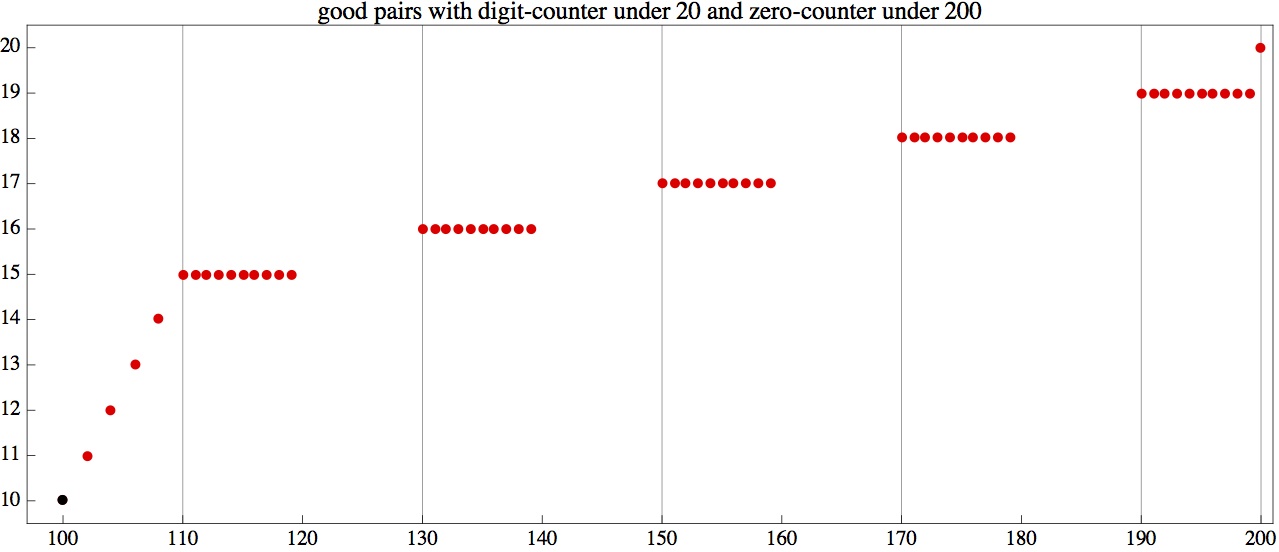
[Back to Problem 1180]
© Copyright 2014 Stan Wagon. Reproduced with permission.