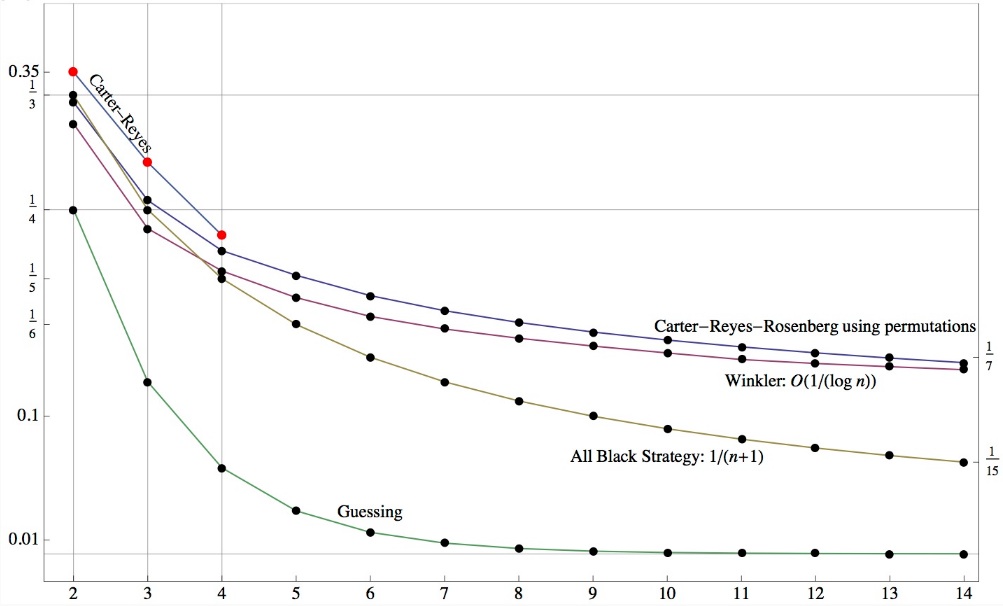
Let the New Zealand strategy (as in New Zealand's "All-Black" sports teams) be the strategy that each person looks for the smallest j so that hat #j for each of the other prisoners is black; the person then states "j." This strategy succeeds iff the all-black vector precedes any vector that is black in all but one position. The vectors are equally likely, so the chance of success is 1/(n + 1).
This was found by: Dan Velleman, Alan Taylor, Joseph DeVincentis, Stephen Morris, Larry Carter, Chen Yan, Aaron Atlee, Eric Egge, Jerry Grossman.
Ding Yuting made an interesting suggestion: Each person looks instead for the smallest j so that he or she sees two whites and one black. Her logic was that WWBB was the most likely 4-tuple.
This last observation is not really relevant, but it inspired me to try the following strategy:
I think I will stop here, in case some of you wish to ponder how to improve the NZ strategy. Perhaps you will find the Winkler strategy; if so, I will congratulate you, as it is hard to find. Or maybe you will find an even better strategy!
Note that the NZ strategy, when it succeeds, finds the lowest black on everyone's head. That is not part of the problem, so one wonders about strategies that do not do that; more on this below.
Note also that it does not require that Alice see any of the other people; she need see only the hats. If everyone were buried under their infinitely many hats, the NZ strategy still works.
I will present here various improved algorithms in the order I learned about them, as this shows the evolution of ideas nicely.
Piotr Zielinski is the only PoW correspondent who found a strategy better than the NZ strategy. He found the Winkler strategy, discussed below, and proved its probability is O (1/log n). Well done.
There are many surprises below, such as a strategy that is better than the NZ strategy for the case
Here is the Winkler strategy (for Peter Winkler, Dartmouth College): The team decides in advance on a certain integer t (the best choice will be described shortly) and then each prisoner assumes that two assertions are true:
(Note that the NZ strategy can be stated: all prisoners work on the assumption that the all-black level precedes any all-but-one-black level.)
Under these assumptions, it is easy for Alice (or anyone else) to find a black hat, since she will know all terms of the sum in (B) except her own. So there is a unique choice from 1, 2, ..., t that yields a sum that is 0 (mod t).
This can be done by taking the derivative and setting it to 0. This yields the equation
Now some complications arise. The main one is that (B), the assumption that the position vector sums to 0 mod t, might be inferior to an assumption that is it congruent to 1, or another target value s, mod t. And then there is the challenge of computing the exact probabilities for each parameter pair t, s for a given n and choosing the best one. I was able to do this by a fairly simple recursion, where we just remove the last person. Thus:
Let F(n, t, s) be the number of hat assignments to the first t levels on n people's heads so that (A) and (B) holds. So the probability is F divided by 2(t n). Here is a simple recursion for F, based on removing the last person — the nth person. Here, Mod[a,b] is the standard least residue upon division by b, lying in {0, ..., b − 1}. Because we index the hats starting with 1, this introduces a small annoyance in the base case, where we need to consider s = 0 as being s = t.
Using this (and caching values), it is very fast to thousands of values. The only real surprises concern the small cases n = 2, 3, or 4.
Surprise #1: For n = 2 or 3, the Winkler strategy, with optimal t
and s, is NOT better than the New Zealand strategy. Best for 2 is
FProb[2,2,0] = 5/16 < 1/3. Best for 3 is FProb[3,3,0] = 121/512 < 1/4.
Surprise #2: For n = 4, the problem posed, the Winkler strategy
using optimal t and target value 0 is NOT better than 1/5. But if t = 4 and s = 1, the success probability is 421/2048, or 0.2056, about 3% greater than 1/5.
For larger values of n the Winkler strategy is an easy winner. For n
= 1000, (t, s) should be (13, 10) and the probability is a rational number with over 3000 digits; it is about 0.068, or 68 times as great as the NZ probability of 1/1001.
Think about this; it is pretty remarkable. Suppose we have 1000 prisoners: the Winkler strategy will then, with probability about 7%, have each one of them picking a black hat!
But maybe there is an even better strategy! Yes, indeed: a recent flurry of activity shows there are more ideas here.
Larry Carter, J-C Reyes, and Joel Rosenberg (San Diego) came up with two new ideas. I think they only did simulations (as opposed to symbolic derivations, which I did), but their ideas are sound.
For n = 3, Winkler with (t, s) = (3, 0) gave 121/512 = 121/512 = 0.236, not better than the NZ strategy. But using t = 4, permutation (342) in
cycle notation, and target sum 3 gives 263/1024, or 0.256. This is
better than 1/4. And now augmenting this with the reset strategy
brings it up to 0.259.
For n = 4, these ideas yield 0.219, with t = 4 and permutation (14)(23). This would increase a bit of course with the reset strategy. Using t = 5 yielded.... Ah: Using t = 6 is best: {0.220287, {5, 3, 1, 4, 6, 2}}
Note that the "permutation" strategy requires that the prisoners enumerate themselves as 1, 2, ..., n in their planning session. The NZ and Winkler strategies do not require this. So these two strategies would work if the hats are visible, but the people are not (perhaps entirely covered by the hats!). But this shows that the Carter et al. strategy is using the additional assumption that the people are visible, so it is to be expected that it gets a better result.
Also, the reset idea means that sometimes the specified black hat will not be the lowest hat on someone's head. This too is new, as the older strategies always found the lowest hat.
More General Searching
And even more recent news: A new record for n = 3, due to J-C Reyes, San Diego.
View the following three 8 × 8 matrices (A, B, C) as a strategy. Alice looks for the first black in each of Bob's and Charlie's piles. If this number-pair is, say, (1, 5), then she chooses the integer in the (1, 5) position in matrix A. Bob and Charlie work the same way, with B and C and the two lowest-hat integers that they see. If one of them does not have a black in the first 8, the method loses.
Simulations show that this succeeds with probability about 0.2617, better than the 0.256 or 0.259 of the permutation strategy. I am still digesting why this works!
The matrices were found by "computer optimization." Remarkable. I did verify by simulation (million trials) that the success rate is the 0.2617.
{{2, 1, 4, 3, 5, 6, 8, 7}, {1, 3, 2, 5, 4, 7, 6, 8},
{3, 2, 1, 4, 6, 5, 7, 4}, {5, 4, 6, 2, 1, 3, 1, 2},
{4, 5, 7, 1, 3, 2, 8, 6}, {7, 6, 5, 8, 2, 1, 4, 3},
{6, 8, 3, 7, 1, 4, 1, 2}, {8, 7, 2, 6, 5, 6, 2, 1}}
{{2, 1, 3, 5, 4, 6, 7, 8}, {1, 3, 2, 4, 6, 5, 8, 7},
{3, 2, 1, 1, 5, 4, 6, 6}, {5, 4, 1, 3, 2, 7, 6, 5},
{4, 5, 6, 2, 1, 3, 7, 7}, {7, 6, 4, 8, 3, 1, 2, 5},
{6, 8, 5, 7, 2, 2, 3, 1}, {8, 7, 8, 6, 1, 3, 1, 2}}
{{2, 1, 3, 5, 4, 6, 7, 8}, {1, 3, 2, 4, 6, 5, 8, 7},
{4, 2, 1, 6, 5, 8, 8, 6}, {4, 5, 4, 2, 1, 7, 6, 7},
{5, 4, 6, 1, 2, 3, 6, 1}, {6, 7, 5, 3, 8, 2, 1, 4},
{8, 6, 7, 6, 3, 1, 4, 2}, {7, 8, 4, 5, 2, 4, 2, 1}}
Note that the rows and columns in these matrices are not permutations. So the universe of possible such triples has 8(3*64) = 10173 entries!
The Winkler method with target sum 0 and t = 3 corresponds to using
this method but with the A = B = C all equal to the 3 × 3 matrix {{1, 3, 2}, {3, 2, 1}, {2, 1, 3}}.
The permutation method can also be formulated in this matrix-strategy context. But the general matrix strategy appears to be much more powerful. Perhaps for t = 100, there is a choice of matrices for which the probability is very large? Of course, the catch is that these matrices are difficult to find.
The Space of All Strategies that Look at t Levels
And now the latest news: Jim Roche discovered that even in the case
of 2 prisoners, Alice and Bob, the NZ strategy with 1/3 chance is NOT
optimal. Here is a strategy that succeeds with probability 22/63 =
0.349.
Have each of Alice and Bob choose according to the following seven rules: This means that if Alice sees all black (0, 0, 0), or (0, 0, 1) or (0, 1, 1), she should choose 1, if she sees (0, 1, 0) or (1, 1, 0) she chooses 2, and if she sees (1, 0, 0) or (1, 0, 1) she chooses 3. Bob does exactly the same.
(0, 0, 0) → 1, (0, 0, 1) → 1, (0, 1, 0) → 2, (0, 1, 1) → 1,
(1, 0, 0) → 3, (1, 0, 1) → 3, (1, 1, 0) → 2
Observe that if Alice should see all white, she knows this strategy is doomed, so, on the off-chance that Bob also sees all white, she moves up to positions 4, 5, 6 instead of 1, 2, 3. This is the "reset" augmentation.
A brute force count of all possibilities shows that without the reset, this wins with chance 22/64 = 0.34375. With the reset, a simple geometric series argument (since we can reset multiple times) increases to 22/63 = 0.3492064. Lovely. And very simple. It takes only a few lines of code to carry out this brute force search. One can vary this by having Alice and Bob follow different strategies. But this asymmetry does not lead to an improvement in this case, (n = 2, t = 3).
Now, if we move up to t = 4, the number of possible strategies grows to the billions. So far, the best I found (also found by others) is 89/256 = 0.347656, which becomes 89/255 = 0.34902 by the reset enhancement. Note the curiosity that 89/256 > 22/63 as one would expect, but when both strategies are augmented by the reset rule, the inequality flips; this is because the augmentation is more valuable the smaller t is. JC Reyes and Larry Carter have gone farther here, with t = 5, finding: 358/1023 = 0.3496. And with t = 6: 1433/4095 = 0.3498. Similarly, for n = 3 and t = 4: 1125/4096 = 0.2746. So we have new records here for n = 2 and n = 3 compared to the earlier work.
So, to finish, we have here a challenging problem in discrete optimization. For a brief moment, I thought LP/ILP could be used, but now I don't think so. But I was right/wrong. Jim Roche has come up with an LP formulation of the problem. It is complicated. We are working on it.
Summary for Two Prisoners
See the plot above for a complete graph of all approaches.
Given t, let T be all the t-tuples of 0s and 1s (in lexicographic order; and the first entry of a tuple is the first hat, etc.).
Find a function F:T → {1, 2, 3, ..., t} which serves as a symmetric strategy with a large chance of success.
The best known are the following (due to Carter and Reyes).
|
n = 2, t = 3
|
11213321
probability = 22/63, as given above
Larry Carter has an argument that shows this is optimal. And that is easy by exhaustion, too.
|
|
n = 2, t = 4
|
1111212144442321
probability = 89/255
Walter Stromquist observed that this is LESS than 22/63 (though the unadorned 22/64 > 89/256, as one would expect). This is now proved optimal by exhaustive search. Also, Walter was able to prove by hand that 89 is an upper bound.
|
|
n = 2, t = 5
|
15452222353531345555222235353131
probability = 358/1023 = 0.349951
|
|
n = 2, t = 6
|
145464641454646424546464445464641111636
3111161661111636311116661
probability = 1433/4096
augments to 1433/4095 = 0.349939
|
|
n = 2, t = 7
|
131146114311431133113311331133112111611
143114111331133113311331166666666666666
663377337733453345666666666666666633773
37733423341
probability = 5734/16383
|
|
n = 2, t = 8
|
513166665131666622226666222266667131666
651316666222266662222666644444444444444
442222222622226666444444444444444422224
622222226628181666681816666222266662222
666681816666818166662222666622226666444
444444444444422228288222286864444444444
4444442222878722228581
probability = 22937/65535 = 0.3499961.
Current record for n = 2. Can anyone break the 0.35 barrier?
|
|
Moving up to n = 3 ...
|
|
n = 3, t = 4
|
142431344322242344332223143322312322111
243221123432311234323112132111143121211
424132314232321244123312431343231123432
311214144333421443244343322331433223123
221312432211232323112343231121221144413
211331242113231221132322322131243221313
3131223141312234
probability = 1125/4096
augments to 64/225 = (8/15)² with the reset strategy
|
Can any of these be improved?
What about t = 9 or larger?
What happens as t → infinity?
Thanks to everyone who contributed. Work is still ongoing and I have hope that some of these results will be improved.
Lots of new developments on this problem have occupied my time recently.
First, some care is needed in how the problem is formulated. Suppose n = 2. Let P be the set of all sequences of 0s and 1s; let N be the natural numbers, {0, 1, 2, 3, ...}. Then a hat assignment is an element of P × P. Suppose one considers a strategy in full abstraction: any function S:P → N, without any care to whether it is constructible. Then one can show, in standard ZFC set theory, that there exists a strategy so that if Alice and Bob use it, then the subset of P × P for which they win has outer measure 1 (it is easy to define a Lebesgue outer measure on P × P having total measure 1).
It follows that the set of games for which they lose cannot be a measurable set of positive measure, so one can say there is no positive probability of losing. This discovery, so counterintuitive that it might lead one to doubt the Axiom of Choice (not me), is by Chris Freiling. The proof is below, but let me first summarize other developments.
Major work has gone on in the case of just two players. Mark Tiefenbruck, J.C. Reyes, Larry Carter, and Joel Rosenberg continued finding and understanding strategies. They found a wonderfully short proof that there is a strategy whose probability of success is exactly 7/20 = 35%. Their work was based on coming up with a sequence of strategies, for fixed number of levels t, where the number of good assignments is 1, 5, 22, 89, 358, and so on, following the alternating recursion 4x + 1 and 4x + 2. Or, in two steps, 16x + 6. Such a sequence, divided by 4t, converges to 7/20. Here is their proof. They also showed how to recursively extend strategies according to the sequence above, which gives the same result.
The 35% Solution (Tiefenbruck, Reyes, Carter, and Rosenberg)
Start with any 3-hat strategy that achieves 22/64 (e.g., 11213321 for the choices on the 8-tuples). Then, if Bob's first three hats are all black or all white, Alice skips them and looks at the next three; Bob does the same. Once Alice finds a level where Bob's hats are not all the same, she uses the 3-hat strategy at that level. There are 60 assignments where at least one of Alice and Bob stops skipping: all but the four where both have all white or all black hats. Ordinarily, the players would have won 21 of these cases — 22 less the one when all six hats are black. If exactly one player (say, Alice) skips this level, then the pair's odds of winning are unchanged because:
-
If Bob had all white, then they weren't going to win anyway.
-
If Bob had all black, then, since he did not skip, they were going to win half the time, and now they still will.
Therefore, the overall probability of success is 21/60 = 7/20. Lovely!
So a prominent question is whether this 7/20 is optimal for the n = 2 case. Recall that prior to their work, it was generally believed that the All-Black strategy, with success rate 1/3, was optimal.
Walter Stromquist has proven the upper bound of 15/40 for this case (whether strategies are symmetric or asymmetric). So the true best lies between 35% and 37.5%.
Using integer-linear programming (ILP, in Mathematica), Jim Roche and I have shown that the value 89 for t = 4 is optimal, even for asymmetric strategies. This was done by hand also, by Walter Stromquist. For t = 5, ILP, using a system with 25,600 variables and breaking it down into 25 subcases, we showed that 358 is the optimal number of good assignments (so the probability is 358/1024) for symmetric strategies. This took about 50 hours of computing time. This was confirmed by Rob Pratt, using a different ILP formulation and different software, and taking only 5 hours, later improved by him to 1.5 hours. But this is only for symmetric strategies.
So to my mind two current questions of great interest are:
-
Is 358/1024 optimal for asymmetric strategies when t = 5?
-
Is 1433/4096 optimal for symmetric or asymmetric strategies when t = 6? Stromquist has a bound of 1496 in this case.
If the answers to 1 and 2 are both YES, that would be solid evidence that the 4x + 1/4x + 2 sequence 1, 5, 22, 89, 358, 1433, ... is optimal, which would be pretty remarkable. If NO, then that means there are more strategies to be found, though Walter's bound is a strong limit showing that we cannot get close to 1/2.
Jim Roche has outlined a proof that, in the case when players must choose their lowest black hat, the best known result is asymptotically optimal for large n:
(1 + o(1))/log2(n)
-
Another important problem supported by the evidence for t ≤ 4 is to prove that asymmetric strategies cannot lead to better results than symmetric strategies.
Walter Stromquist has expressed his upper bound work in terms of an ILP, and also in terms of a Hamming distance problem. The ILP, for t = 5, does not have very many variables, but I could not get it to stop in reasonable time.
Chris Freiling's Nonconstructive Strategy
Theorem (C. Freiling): Assume AC. Then the success set of the following strategy is not measurable.
Proof: Let A × B be the space of hat sequences for the two players. Well-order the closed subsets of A × B that have positive measure. The cardinality of this collection of sets is the same as the size of the real numbers, c. So the well-ordering can have the property that any initial segment has size less than c.
Now go through this list of sets, S0, S1, S2, ......, Sα, ... At any given stage, α, we will choose one pair of hat sequences, (x, y) in Sα, where neither x nor y are all zeros and where the strategy has not yet been determined on either x or y. Then we will make sure that if B sees x then B chooses a bit position where y has the value 1, and similarly if A sees y then A chooses a bit position where x has the value 1. In other words, if (x, y) are chosen, then the players go free.
To see how to choose x and y, we use Fubini's Theorem. Since Sα has positive measure, there is a positive measure of x's each of which has a positive measure of y's such that (x, y) is in Sα. This set of x's then has size c, so we can find at least one which has not been previously considered. Then the corresponding set of y's also has size c, so we can find one of these that has not been previously considered.
At the end we have a strategy where the losing positions do not contain any closed set of positive measure. It follows that the losing set cannot be a set of positive Lebesgue measure, so, in a certain sense, there is zero chance of losing.
Now, one might say that in posing the problem the use of the word probability indicates that one wants a strategy that is a measurable function, so that the set of winning positions is a measurable set.
Thanks to everyone for their enthusiasm for this addictive problem.
[Back to Problem 1179]
© Copyright 2014 Stan Wagon. Reproduced with permission.