Solution
For the problem posed, the answer is 8. The solution is quite pretty:
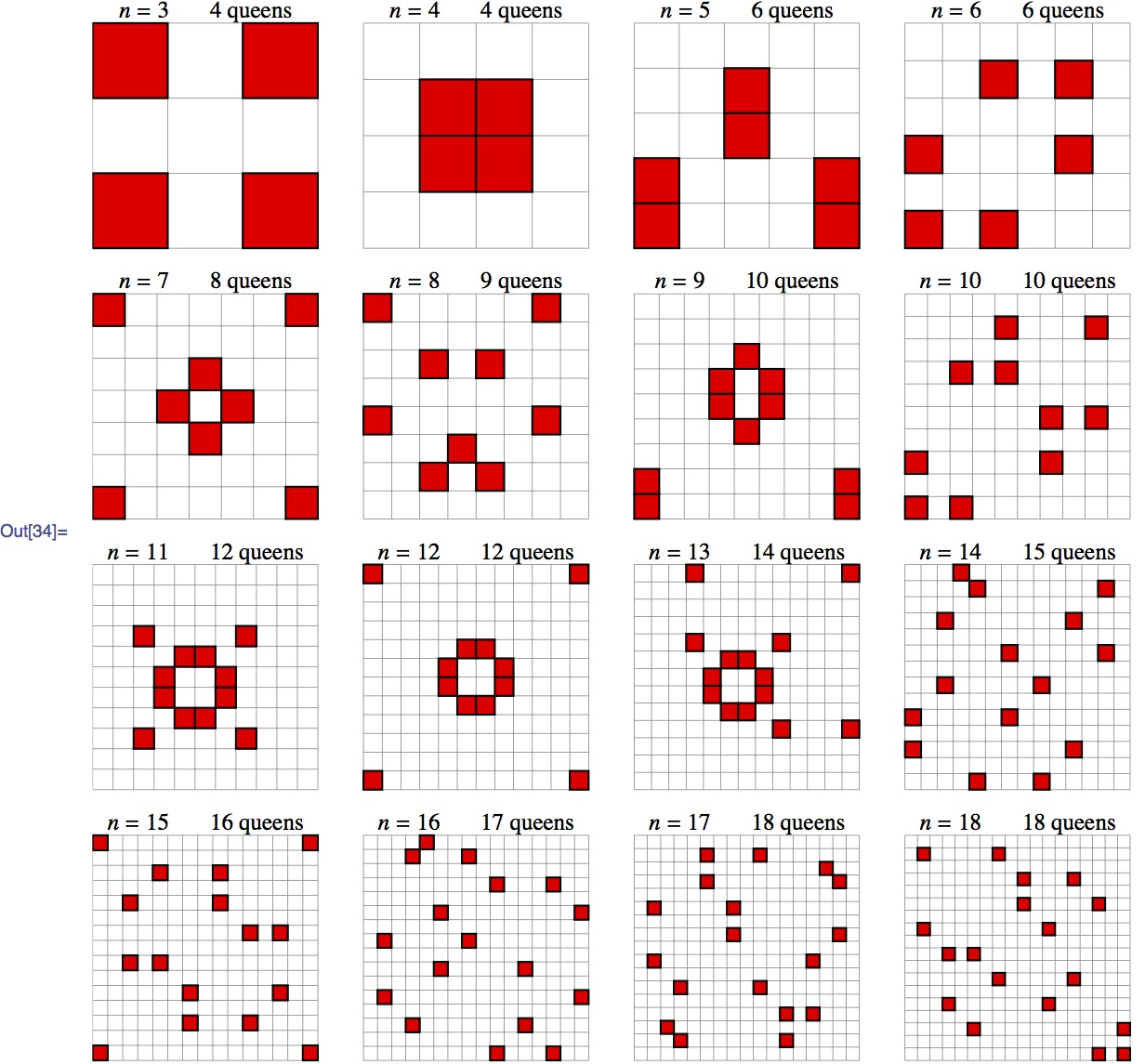
This shows optimal solutions for all n up to 18. After the Amer. Math. Monthly paper appeared, Rob Pratt used ILP (integer-linear programming) to resolve many unresolved cases; the cases 15, 16, 17, 18 in the diagram are his. I implemented his approach in Mathematica and that yielded results up to 14 (which of course he got first), also included in the diagram. Then I added some symmetry conditions, so that I got some nicely symmetric results; the solutions up to n = 13 all show some of that symmetry.
For more on how Pratt set up the ILP equations, download this PDF.
The problem posed was solved by Jonathan Foster, Xie Jia (Beijing), and Wang Yue (Beijing). One 11-marker solution was submitted. They found the same symmetric solution that I found (and might likely have been known).
For the famous Dudeney no-3-in-line problem, a solution (with 2n markers) is known up to and including n = 46, and a few values beyond that. Can ILP settle some of the unknown cases? Known solutions can be seen in this Wolfram Interactive Demonstration.
See also A. Flammenkamp's "The No-Three-in-Line Problem" (Mar 3, 1998). Flammenkamp observes that he used a "sophisticated branch-and-bound" algorithm. This makes it seem like ILP might be able to work too, but a naive approach, using constraints for all possible lines, did not get very far.
[Back to Problem 1178]
© Copyright 2014 Stan Wagon. Reproduced with permission.