Solution
The problem was about finding a small set so that the address of each point is unique. The best known was Gary Gordon's 16 points:
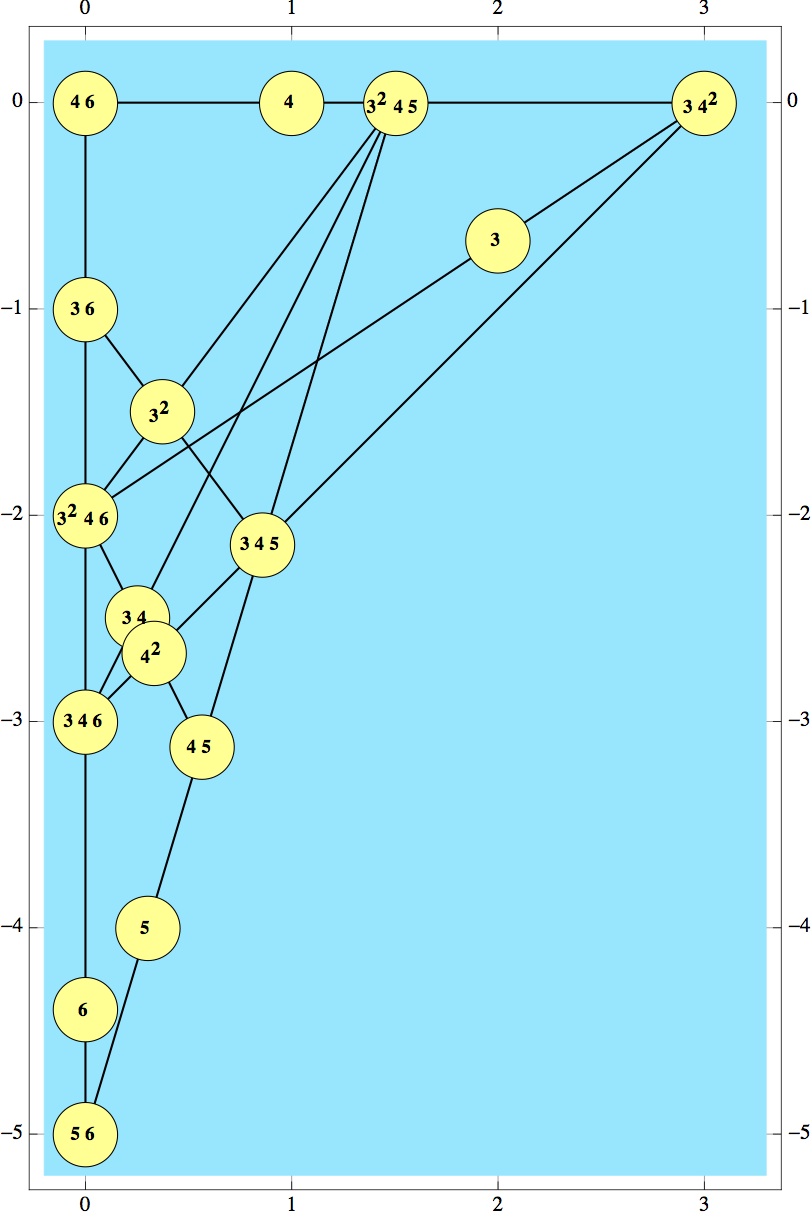
Joseph DeVincentis found a 13-point solution:
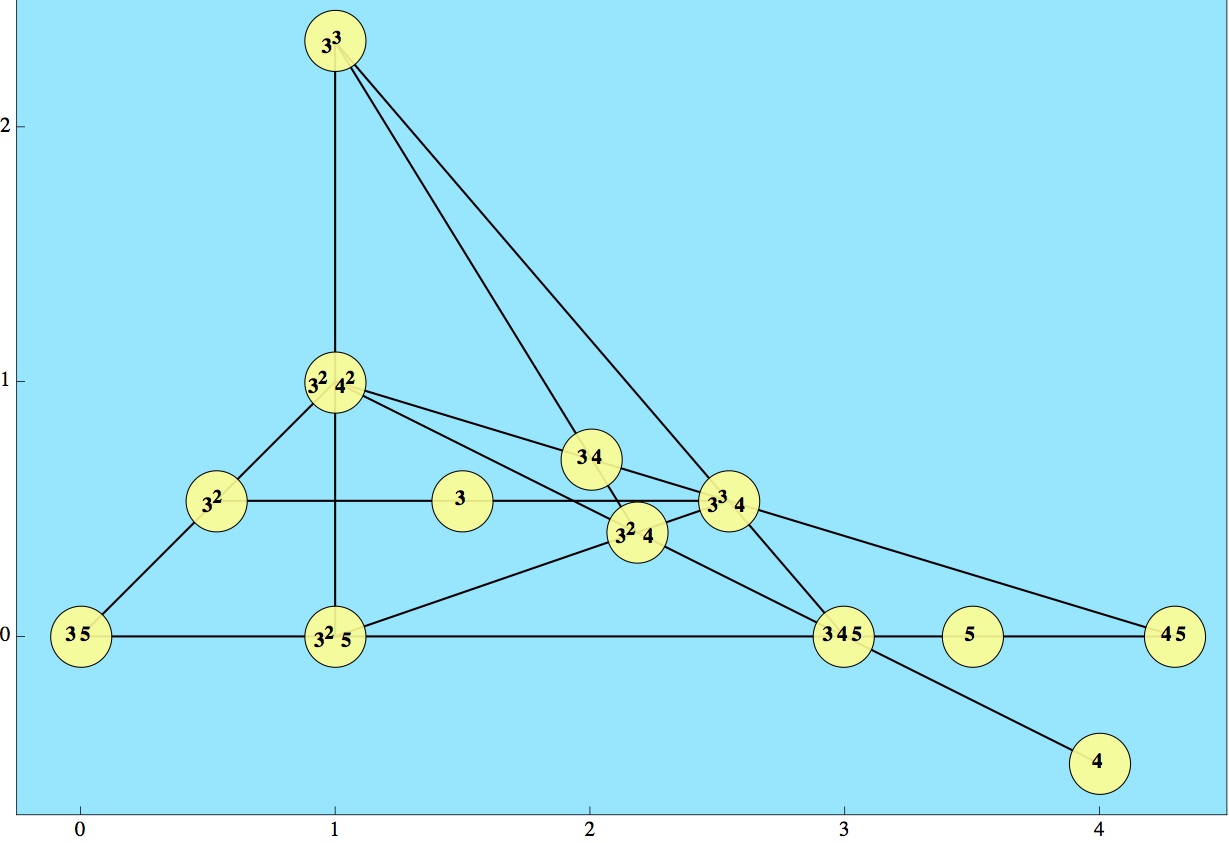
This is easily described as
{{0, 0}, {0, 4}, {0, 16}, {1, 13},
{1, 16}, {3, 4}, 2, 16}, {24, 4}}
Xie Jia (Peking University) found a different 13-point solution:
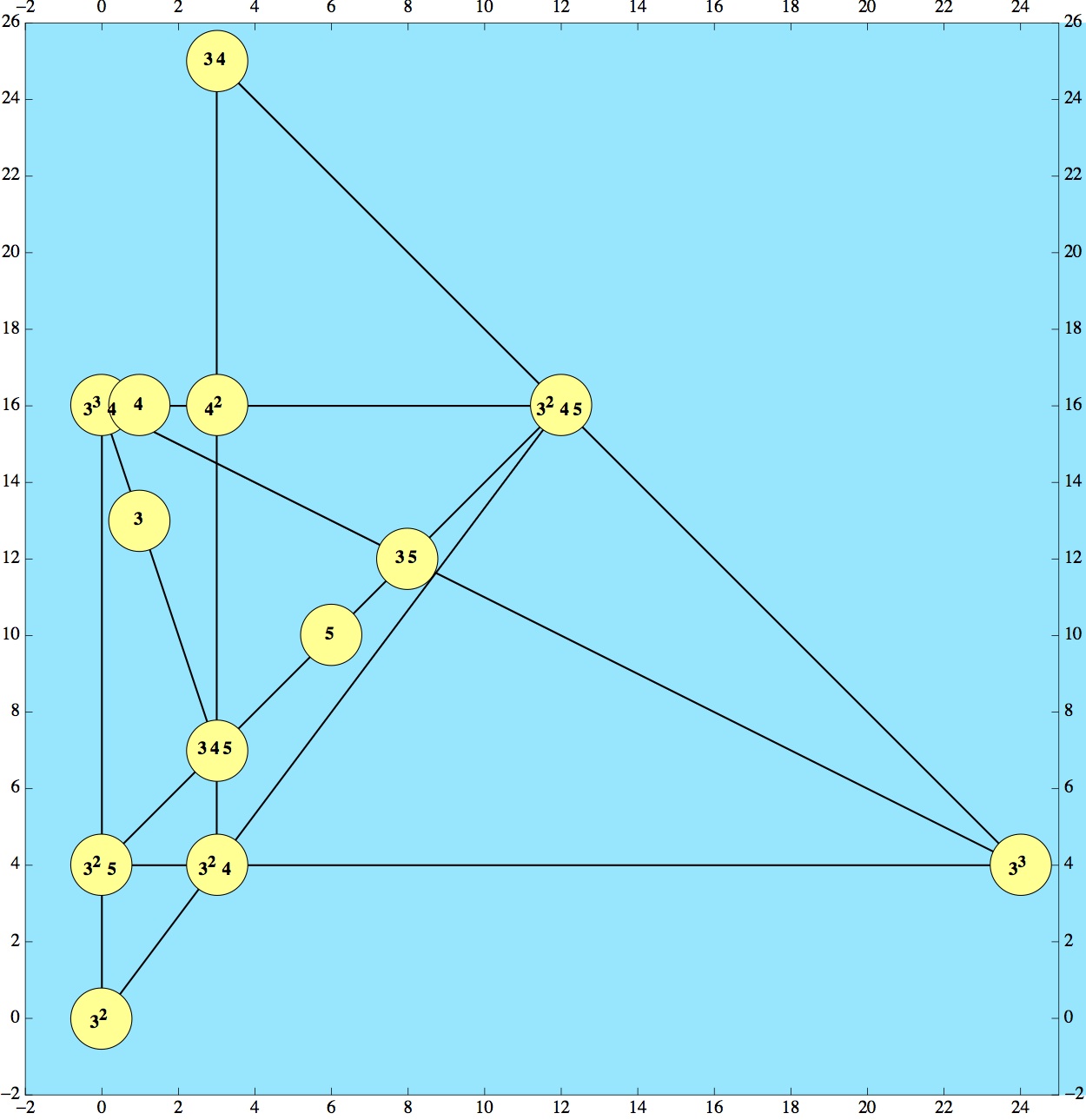
And two 18-point solutions were submitted.
Gary Gordon observes that the problem has connections with matroid theory.
As for finding infinitely many points, I do not know if there is a direct solution that lists the points, but an induction works to get a sequence of points having address 3, 3², 3³, and so on, where I use the exponential notation for addresses.
Proof:
Let H(n) for a point set (P1, P2, ...) of at least n points be the assertion that, for i ≤ n, each Pi has address 3i, and each Pj for j > n is on no 4-point line and at most j 3-point lines.
Then H(1) holds for any three points P1, P2, P3 on a line. Now inductively build up this triplet so as to preserve and extend H. Given that H(n) holds for (P1, P2, ..., Pn, ..., Pm), define Pm + 1, Pm + 2, and so on as needed so that the new points
-
introduce collinearities so as to bring the address of Pn + 1 up to 3(n + 1);
-
introduce no collinearities other than those of (A).
Since (B) eliminates a finite collection of lines, there will always be new points available to get (A) to hold. After infinitely many steps, we will have a countably infinite set for which H(n) is true for all n.
Is there a more constructive approach?
Update: Roger MadPlume, a math graduate student at the University of Montana, has found an 11-point solution, and proved that it is minimal!
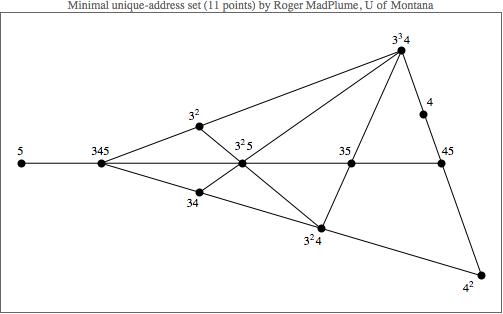
If anyone wants to see his proof of minimality, contact me for his email address.
[Back to Problem 1176]
© Copyright 2014 Stan Wagon. Reproduced with permission.