Solution
I received no comments on the hex queen coloring problem. So either you found it too easy or too hard or too uninteresting. Dan Ullman and I think the problem is a nice one and we have just submitted it to a journal, so I will not post the solution here. I am curious whether anyone solved it.
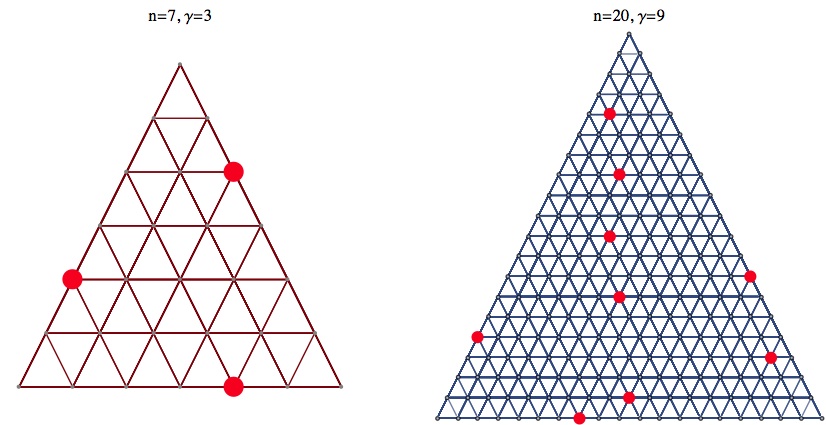
As for the various other hex queen problems, thanks again to Rob Pratt for finding the miracle at n = 20. In general, one can dominate the n + 2 queen graph by just adding in an apex to a solution for the n-graph. Q(6) can be dominated with 3 (just take the central vertical line of 3), and — in a bit of a surprise — Q(7) can be dominated with 3, also:
So the pattern rising from 6 goes
3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9
But Rob Pratt found that new miracle at 20, which can be dominated with 9, as opposed to the 10 that I expected (image at same link). Presumably there are more miracles like this.
In any case, this shows that for n ≥ 18 the upper bounds are as follows:
9, 9, 9, 10, 10, 11, 11, 12, 12
So letting γ denote the domination number,
γ(Q(n)) =
|
Floor[(n + 1)/2]
|
for 1 ≤ n ≤ 6
|
|
Floor[n/2]
|
for 7 ≤ n ≤ 19
|
|
Floor[(n − 1)/2]
|
for 19 ≤ n ≤ 20
|
One wonders where the next miracle of hex queen domination occurs, and of course, if there are infinitely many such reductions.
[Back to Problem 1166]
© Copyright 2013 Stan Wagon. Reproduced with permission.