Solution
This was solved by Michael Elgersma and Franz Pichler, and of course Brian Trial, who found the original integer solution.
The solution is 1, 2, 3, 4:
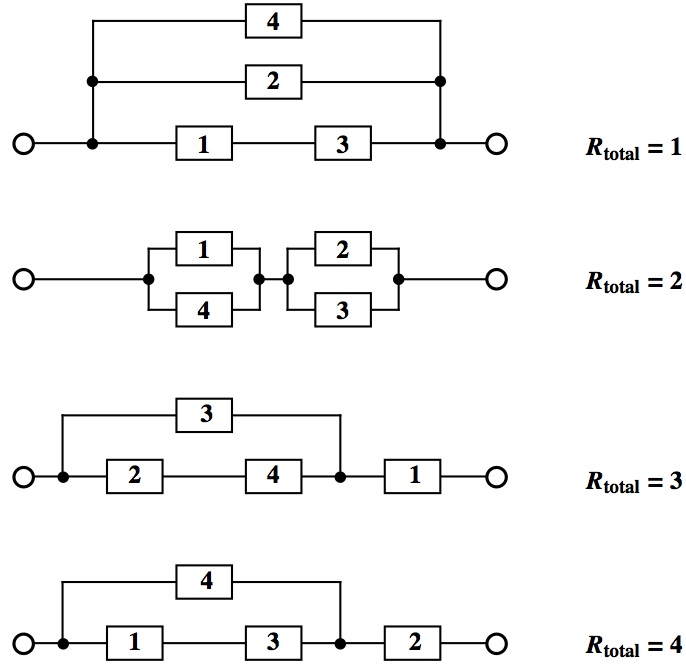
What is remarkable for this problem is that the solution is unique up to scaling and reciprocals. That is, there is only one set of four series-parallel networks and four integer resistances that are self-replicating in this way. Proving this required me to examine 230,000 cases, using Mathematica's equation-solving tools to check for a solution. There are many solutions in algebraic numbers and even one using {1, Sqrt[2], Sqrt[2], 2}, but only one using integers. Note that reciprocal and scaling of 1, 2, 3, 4 leads to 3, 4, 6, 12, which is not really a new solution. We have not checked for solutions using negative numbers; possibly there are some.
Open questions here are:
Is it true that, for every n ≥ 4, there is a self-replicating set of integer resistances? (Brian Trial found such for n = 5 and a couple of larger values.)
Is it true that, for every n ≥ 4, the resistances 1, 2, 3, 4, ..., n can be used to get a self-replicating set of networks?
The On-Line Encyclopedia of Integer Sequences lists two sequences, A000084 and A193205, which are helpful if you are trying to program these in a way that checks all cases.
[Back to Problem 1165]
© Copyright 2013 Stan Wagon. Reproduced with permission.